
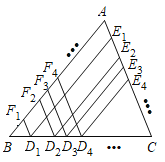
【题目】如图,在△ABC中,AB=5,AC=4,若进行一下操作,在边BC上从左到右一次取点D1、D2、D3、D4…;过点D1作AB、AC的平行线分别交于AC、AB与点E1、F1;过点D2作AB、AC的平行线分别交于AC、AB于点E2、F2;过点D3作AB、AC的平行线分别交于AC、AB于点E3、F3…,则4(D1E1+D2E2+…+D2019E2019)+5(D1F1+D2F2+…+D2019F2019)=______.
【答案】40380.
【解析】
由D1E1∥AB ,D1F1∥AC,可得△CD1E1∽△CBA,△BD1F1∽△BCA,根据相似三角形的对应边成比例结合AB=5,AC=4,可得![]() ,
,![]() ,再根据CD1+BD1=BC,可求得4D1E1+5D1F1=20,同理可得4D2E2+5D2F2=20,4D3E3+5D3F3=20,…,4D2019E2019+5D2019F2019=20,继而可求得答案.
,再根据CD1+BD1=BC,可求得4D1E1+5D1F1=20,同理可得4D2E2+5D2F2=20,4D3E3+5D3F3=20,…,4D2019E2019+5D2019F2019=20,继而可求得答案.
∵D1E1∥AB ,D1F1∥AC,
∴△CD1E1∽△CBA,△BD1F1∽△BCA,
∴![]() ,
, ![]() ,
,
∵AB=5,AC=4,
∴![]() ,
,![]() ,
,
又∵CD1+BD1=BC,
∴![]() ,
,
∴4D1E1+5D1F1=20,
同理:4D2E2+5D2F2=20,4D3E3+5D3F3=20,…,4D2019E2019+5D2019F2019=20,
∴4(D1E1+D2E2+…+D2019E2019)+5(D1F1+D2F2+…+D2019F2019)=2019×20=40380,
故答案为:40380.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某校随机抽取部分学生,就“学习习惯”进行调查,将“对自己做错题进行整理、分析、改正”(选项为:很少、有时、常常、总是)的调查数据进行了整理,绘制成部分统计图如下:

请根据图中信息,解答下列问题:
(1)该调查的样本容量为________, ![]() =________%,
=________%, ![]() =________%,“常常”对应扇形的圆心角的度数为__________;
=________%,“常常”对应扇形的圆心角的度数为__________;
(2)请你补全条形统计图;
(3)若该校有3200名学生,请你估计其中“总是”对错题进行整理、分析、改正的
学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在平行四边形ABCD的边AB,CD上截取AF,CE,使得AF=CE,连接EF,点M,N是线段EF上两点,且EM=FN,连接AN,CM.
(1)求证:△AFN≌△CEM;
(2)若∠CMF=107°,∠CEM=72°,求∠NAF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级八个班共有320名学生,男女生人数大致相同,调查小组为调查学生的体质健康水平,开展了一次调查研究,请将下面的过程补全.
收集数据
(1)调查小组计划选取40名学生的体质健康测试成绩作为样本,下面的取样方法中,合理的是_____(填字母);
A.抽取九年级1班、2班各20名学生的体质健康测试成绩组成样本
B.抽取各班体育成绩较好的学生共40名学生的体质健康测试成绩组成样本
C.从年级中按学号随机选取男女生各20名学生学生的体质健康测试成绩组成样本
整理、描述数据
(2)抽样方法确定后,调查小组获得了40名学生的体质健康测试成绩如下:
![]()
整理数据,如下表所示:
2019年九年级部分学生学生的体质健康测试成绩统计表
体质成绩范围 | 学生人数 | 体质成绩范围 | 学生人数 |
50≤x<55 | 1 | 75≤x<80 | |
55≤x<60 | 1 | 80≤x<85 | ( ) |
60≤x<65 | 2 | 85≤x<90 | ( ) |
65≤x<70 | 2 | 90≤x<95 | 5 |
70≤x<75 | 4 | 95≤x<100 | 2 |

分析数据,得出结论
调查小组将统计后的数据与去年同期九年级学生的体质健康测试成绩(上方直方图)进行对比分析.
(3)若规定80分以上(包括80分)为合格健康体质.从合格率的角度看,这两年的学生哪年体质测试成绩好?
(4)体育老师计划根据2019年的统计数据安排75分以下的同学参加体质加强训练项目,则全年级约有_______名同学参加此项目.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黄岩某校搬迁后,需要增加教师和学生的寝室数量,寝室有三类,分别为单人间(供一个人住宿),双人间(供两个人住宿),四人间(供四个人住宿).因实际需要,单人间的数量在20至30之间(包括20和30),且四人间的数量是双人间的5倍.
(1)若2018年学校寝室数为64个,以后逐年增加,预计2020年寝室数达到121个,求2018至2020年寝室数量的年平均增长率;
(2)若三类不同的寝室的总数为121个,则最多可供多少师生住宿?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面内的两条直线l1、l2,点A、B在直线l2上,过点A、B两点分别作直线l1的垂线,垂足分别为A1、B1,我们把线段A1B1叫做线段AB在直线l2上的正投影,其长度可记作T(AB,CD)或T(AB,l2),特别地,线段AC在直线l2上的正投影就是线段A1C,请依据上述定义解决如下问题.
(1)如图1,在锐角△ABC中,AB=5,T(AC,AB)=3,则T(BC,AB)= ;
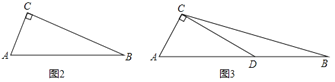
(2)如图2,在Rt△ABC中,∠ACB=90°,T(AC,AB)=4,T(BC,AB)=9,求△ABC的面积;
(3)如图3,在钝角△ABC中,∠A=60°,点D在AB边上,∠ACD=90°,T(AD,AC)=2,T(BC,AB)=6,求T(BC,CD).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校八年级的体育老师为了了解本年级学生喜欢球类运动的情况,抽取了该年级部分学生对篮球、足球、排球、乒乓球的爱好情况进行了调查,并将调查结果绘制成如图两幅不完整的统计图(说明:每位学生只选一种自己最喜欢的一种球类),请根据这两幅图形解答下列问题:
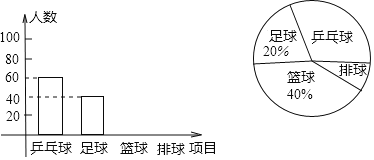
(1)在本次调查中,体育老师一共调查了多少名学生?
(2)将两个不完整的统计图补充完整;
(3)求出乒乓球在扇形中所占的圆心角的度数?
(4)已知该校有760名学生,请你根据调查结果估计爱好足球和排球的学生共计多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】天虹超市购进甲、乙两种水果,已知 1 千克甲种水果的进价比 1 千克乙种水果的进价多 4 元,购进 2
千克甲种水果与 3 千克乙种水果共需 28 元.
求甲种水果的进价为每千克多少元?
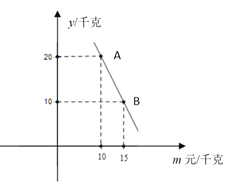
(2)经市场调查发现,甲种水果每天销售量 y(千克)与售价 m(元/千克)之间满足如图所示的函数关系,求 y
与 m 之间的函数关系;
(3)在(2)的条件下,为减少库存,每天甲种水果的销售量不能低于 16 千克,当甲种水果的售价定为多少元时,才能使每天销售甲种水果的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
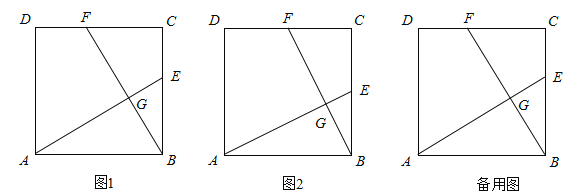
【题目】正方形ABCD的边长为4,点E在BC上,点F在CD上,且CF=BE,AE与BF交于G点.
(1)如图1,求证:①AE=BF,②AE⊥BF.
(2)连接CG并延长交AB于点H,
①若点E为BC的中点(如图2),求BH的长;
②若点E在BC的边上滑动(不与B、C重合),当CG取得最小值时,求BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com