练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，正方形ABCD中，点E是AD边的中点，BD，CE交于点H，BE、AH交于点G，则下列结论：

    ①∠ABE＝∠DCE；②∠AHB＝∠EHD；③S△BHE＝S△CHD；④AG⊥BE．其中正确的是（ ）

    A.①③B.①②③④C.①②③D.①③④

    【答案】B

    【解析】

    根据正方形的性质证得，推出，可知①正确；证明，再根据对顶角相等即可得到，可知②正确；根据，求出，推出，即，故③正确；利用正方形性质证，求得，推出；求出，求得故④正确．

    解：四边形是正方形，是边上的中点，

    ，，，

    ，

    ，

    故①正确；

    ∵四边形ABCD是正方形，

    ∴AB=BC, ∠ABD=∠CBD，

    ∵BH=BH，

    ∴，

    ，

    ，

    ，

    故②正确；

    ，

    ，

    ，

    即，

    故③正确；

    四边形是正方形，

    ，，，

    ，

    ，

    ，

    ，

    ，

    ，

    ，

    故④正确；

    故选：．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知等腰三角形一腰上的中线将三角形的周长分为9cm和15cm两部分，求这个等腰三角形的底边长和腰长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ACB＝90°，过点C的直线MN∥AB，D为AB边上一点，过点D作DE⊥BC，交直线MN于E，垂足为F，连接CD，BE.

    （1）求证：CE＝AD；

    （2）当D为AB中点时，四边形BECD是什么特殊四边形？说明你的理由；

    （3）若D为AB中点，则当∠A的大小满足什么条件时，四边形BECD是正方形？请说明你的理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△BAD是由△BEC在平面内绕点B旋转60°而得，且AB⊥BC，BE＝CE，连接DE.

    （1）求证：△BDE≌△BCE；

    （2）试判断四边形ABED的形状，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，AD是中线，∠BAD=∠B+∠C，tan∠ABC=，则tan∠BAD=________．

    【答案】

    【解析】延长AD到E,使AD=DE,CF ,

    在与,

    , ,所以，

    是等腰三角形，s

    设EM= x,DE=11,MC=10,

    ,

    ,

    x=,

    tan∠BAD=.

    故答案为.

    点睛：倍长中线法构造全等三角形,如图，AD是中线，令AD=DE,则ADC全等EBD.

    【题型】填空题
    【结束】
    21

    【题目】先化简，再求值： ÷（-a+2），其中a=2sin60°+3tan45°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了解青少年形体情况，现随机抽查了若干名初中学生坐姿、站姿、走姿的好坏情况（如果一个学生有一种以上不良姿势，以他最突出的一种作记载），并将统计结果绘制了如下两幅不完整的统计图，请根据图中所给信息解答下列问题：

    （1）求这次被抽查形体测评的学生一共有多少人？

    （2）求在被调查的学生中三姿良好的学生人数，并将条形统计图补充完整；

    （3）若全市有5万名初中生，那么估计全市初中生中，坐姿和站姿不良的学生共有多少人？

    【答案】（1）500名；（2）75名；（3）2.5万

    【解析】试题分析：（1）用类型人数除以所占百分比就是总人数.(2)用总人数乘以15%.

    (3) 坐姿和站姿不良的学生的学生的百分比乘以总人数.

    试题解析：

    （1）解：100÷20%=500（名），

    答：这次被抽查形体测评的学生一共是500名；

    （2）解：三姿良好的学生人数：500×15%=75名，

    补全统计图如图所示；

    （3）解：5万×（20%+30%）=2.5万，

    答：全市初中生中，坐姿和站姿不良的学生有2.5万人．

    【题型】解答题
    【结束】
    24

    【题目】如图，矩形ABCD中，P为AD边上一点，沿直线BP将△ABP翻折至△EBP（点A的对应点为点E），PE与CD相交于点O，且OE=OD．

    （1）求证：PE=DH；

    （2）若AB=10，BC=8，求DP的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知、是关于的方程的两个不相等的实数根.

    (1)求实数的取值范围;

    (2)已知等腰的一边长为7，若、恰好是另外两边长，求这个三角形的周长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

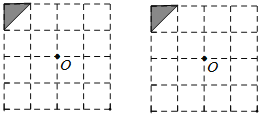
    【题目】(1)如图是一个4×4的正方形网格，每个小正方形的边长均为1.请在网格中以左上角的三角形为基本图形，通过平移、对称或旋转，设计两个精美图案，使其满足：①既是轴对称图形，又能以点为旋转中心旋转而得到；②所作图案用阴影标识，且阴影部分面积为4.

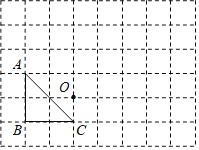
    (2)如图，的三个顶点和点都在正方形网格的格点上，每个小正方形的边长都为1.

    ①将先向右平移4个单位，再向上平移2个单位得到，请画出；

    ②请画出，使和关于点成中心对称；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

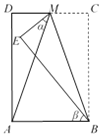
    【题目】如图，在长方形ABCD中，点M为CD中点，将△MBC沿BM翻折至△MBE，若∠AME ＝ α，∠ABE ＝ β，则 α 与 β 之间的数量关系为________．

    查看答案和解析>>

    同步练习册答案