
ЎҫМвДҝЎҝИзНјЈ¬ФЪЖҪГжЦұҪЗЧшұкПөЦРЈ¬ПЯ¶О![]() өД¶Лөг¶јФЪНшёсПЯөДҪ»өгЙПЈЁГҝёцРЎ·Ҫёс¶јКЗұЯіӨОӘ1ёцөҘО»іӨ¶ИөДХэ·ҪРОЈ©Ј¬°ҙТӘЗуНкіЙПВБРИООсЈ®
өД¶Лөг¶јФЪНшёсПЯөДҪ»өгЙПЈЁГҝёцРЎ·Ҫёс¶јКЗұЯіӨОӘ1ёцөҘО»іӨ¶ИөДХэ·ҪРОЈ©Ј¬°ҙТӘЗуНкіЙПВБРИООсЈ®
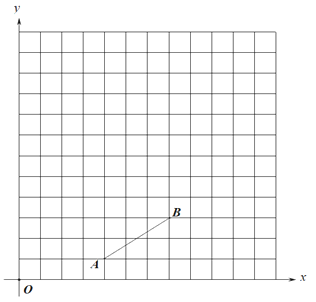
ЈЁ1Ј©ТФөг![]() ОӘРэЧӘЦРРДЈ¬Ҫ«ПЯ¶О
ОӘРэЧӘЦРРДЈ¬Ҫ«ПЯ¶О![]() ДжКұХлРэЧӘ
ДжКұХлРэЧӘ![]() Ј¬өГөҪПЯ¶О
Ј¬өГөҪПЯ¶О![]() Ј¬»ӯіцПЯ¶О
Ј¬»ӯіцПЯ¶О![]() Ј»
Ј»
ЈЁ2Ј©ТФФӯөг![]() ОӘО»ЛЖЦРРДЈ¬Ҫ«ПЯ¶О
ОӘО»ЛЖЦРРДЈ¬Ҫ«ПЯ¶О![]() ФЪөЪТ»ПуПЮА©ҙу3ұ¶Ј¬өГөҪПЯ¶О
ФЪөЪТ»ПуПЮА©ҙу3ұ¶Ј¬өГөҪПЯ¶О![]() Ј¬»ӯіцПЯ¶О
Ј¬»ӯіцПЯ¶О![]() Ј»ЈЁөг
Ј»ЈЁөг![]() Ј¬
Ј¬![]() өД¶ФУҰөг·ЦұрКЗ
өД¶ФУҰөг·ЦұрКЗ![]() Ј¬
Ј¬![]() Ј©
Ј©
ЈЁ3Ј©ФЪПЯ¶О![]() ЙПСЎФсТ»өг
ЙПСЎФсТ»өг![]() Ј¬К№өГТФөг
Ј¬К№өГТФөг![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() ОӘ¶ҘөгөДЛДұЯРОКЗЖҪРРЛДұЯРОЈ¬ЗлЦұҪУРҙіцөг
ОӘ¶ҘөгөДЛДұЯРОКЗЖҪРРЛДұЯРОЈ¬ЗлЦұҪУРҙіцөг![]() өДЧшұкЈ®
өДЧшұкЈ®
Ўҫҙр°ёЎҝЈЁ1Ј©ПЯ¶О![]() ИзНјЛщКҫ.јыҪвОцЈ»ЈЁ2Ј©ПЯ¶О
ИзНјЛщКҫ.јыҪвОцЈ»ЈЁ2Ј©ПЯ¶О![]() ИзНјЛщКҫ. јыҪвОцЈ»ЈЁ3Ј©
ИзНјЛщКҫ. јыҪвОцЈ»ЈЁ3Ј©![]() Ј®
Ј®
ЎҫҪвОцЎҝ
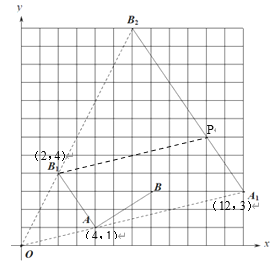
ЈЁ1Ј©ЧчіцөгBИЖөгAДжКұХлРэЧӘ90ЎгөГөҪөД¶ФУҰөгB1Ј¬Б¬ҪУAB1јҙҝЙЈ»
ЈЁ2Ј©ТФөгOОӘО»ЛЖЦРРДЈ¬Ҫ«ПЯ¶ОAB1·ЕҙуОӘФӯАҙөД3ұ¶Ј¬јҙҝЙ»ӯіцПЯ¶ОA1B2Ј»
ЈЁ3Ј©ПИИ·¶Ёөг![]() өДҫЯМеО»ЦГЈ¬ФЩёщҫЭЦұҪЗЧшұкПөәННшёсМШөгјҙҝЙИ·¶Ё
өДҫЯМеО»ЦГЈ¬ФЩёщҫЭЦұҪЗЧшұкПөәННшёсМШөгјҙҝЙИ·¶Ё![]() өДЧшұкЈ®
өДЧшұкЈ®
ЈЁ1Ј©ПЯ¶О![]() ИзНјЛщКҫ.
ИзНјЛщКҫ.
ЈЁ2Ј©ПЯ¶О![]() ИзНјЛщКҫ.
ИзНјЛщКҫ.
ЈЁ3Ј©ИзНјЈ¬№эөгBЧчBPЎОAA1Ј¬Ҫ»A1B1УЪөгPЈЁөгPНшёсПЯөДҪ»өгЙПЈ©Ј¬
УЙМвЈЁ2Ј©ҝЙЦӘЈәAB1ЎОA1PЈ¬ҙЛКұЛДұЯРОAA1PB1јҙОӘТФөг![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() ОӘ¶ҘөгөДЖҪРРЛДұЯРОЈ¬
ОӘ¶ҘөгөДЖҪРРЛДұЯРОЈ¬
ёщҫЭЦұҪЗЧшұкПөәННшёсМШөгҝЙЦӘЈәөгAЈЁ4,1Ј©Ј¬өгB1ЈЁ2,4Ј©Ј¬өгA1ЈЁ12,3Ј©Ј¬өг![]() өДЧшұк
өДЧшұк![]() .
.



| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
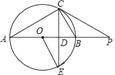
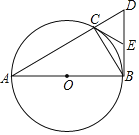
ЎҫМвДҝЎҝИзНјЈ¬ТСЦӘЈ¬ABКЗЎСOөДЦұҫ¶Ј¬өгPФЪABөДСУіӨПЯЙПЈ¬ПТCEҪ»ABУЪөгЈ¬Б¬ҪбOEЈ¬ACЈ¬ЗТЎПP=ЎПEЈ¬ЎПPOE=2ЎПCABЈ®
ЈЁ1Ј©ЗуЦӨЈәCEЎНABЈ»
ЈЁ2Ј©ЗуЦӨЈәPCКЗЎСOөДЗРПЯЈ»
ЈЁ3Ј©ИфBD=2ODЈ¬ЗТPB=9Ј¬ЗуЎСOөД°лҫ¶іӨәНtanЎПPөДЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
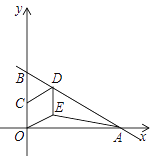
ЎҫМвДҝЎҝИзНјЈ¬ЦұПЯ![]() УлxЦбЎўyЦб·ЦұрҪ»УЪAЈ¬BБҪөгЈ¬CКЗOBөДЦРөгЈ¬DКЗABЙПТ»өгЈ¬ЛДұЯРОOEDCКЗБвРОЈ¬ФтЎчOAEөДГж»эОӘ________Ј®
УлxЦбЎўyЦб·ЦұрҪ»УЪAЈ¬BБҪөгЈ¬CКЗOBөДЦРөгЈ¬DКЗABЙПТ»өгЈ¬ЛДұЯРОOEDCКЗБвРОЈ¬ФтЎчOAEөДГж»эОӘ________Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ТСЦӘ![]() ДЪУЪ
ДЪУЪ![]() Ј¬
Ј¬![]() ОӘ
ОӘ![]() өДЦұҫ¶Ј¬
өДЦұҫ¶Ј¬![]() Ј¬Ҫ»
Ј¬Ҫ»![]() өДСУіӨПЯУЪөг
өДСУіӨПЯУЪөг![]() Ј®
Ј®
ЈЁ1Ј©![]() ОӘ
ОӘ![]() өДЦРөгЈ¬Б¬ҪУ
өДЦРөгЈ¬Б¬ҪУ![]() Ј¬ЗуЦӨЈә
Ј¬ЗуЦӨЈә![]() КЗ
КЗ![]() өДЗРПЯЈ»
өДЗРПЯЈ»
ЈЁ2Ј©Иф![]() Ј¬Зу
Ј¬Зу![]() өДҙуРЎЈ®
өДҙуРЎЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘөгAЈЁ1Ј¬1Ј©ФЪЕЧОпПЯyЈҪx2+ЈЁ2m+1Ј©x©Ғn©Ғ1ЙП
ЈЁ1Ј©ЗуmЎўnөД№ШПөКҪЈ»
ЈЁ2Ј©ИфёГЕЧОпПЯөД¶ҘөгФЪxЦбЙПЈ¬ЗуіцЛьөДҪвОцКҪЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝЗу1Ј«2Ј«22Ј«23Ј«ЎӯЈ«22020өДЦөЈ¬ҝЙБоSЈҪ1Ј«2Ј«22Ј«23Ј«ЎӯЈ«22020Ј¬Фт2SЈҪ2Ј«22Ј«23Ј«24Ј«ЎӯЈ«22021Ј¬ТтҙЛ2SЈӯSЈҪ22021Јӯ1Ј®·ВХХТФЙПНЖАнЈ¬јЖЛгіц1Ј«2020Ј«20202Ј«20203Ј«ЎӯЈ«20202020өДЦөОӘЈЁ Ј©
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘЕЧОпПЯ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬ЎӯЈ¬
Ј¬ЎӯЈ¬![]() ЈЁnОӘХэХыКэЈ©Ј¬өгA(0Ј¬1)Ј®
ЈЁnОӘХэХыКэЈ©Ј¬өгA(0Ј¬1)Ј®
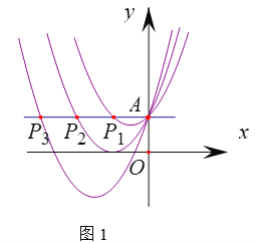
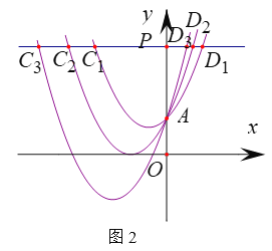
ЈЁ1Ј©ИзНј1Ј¬№эөгAЧчyЦбҙ№ПЯЈ¬·ЦұрҪ»ЕЧОпПЯ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬ЎӯЈ¬
Ј¬ЎӯЈ¬![]() УЪөг
УЪөг![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬ЎӯЈ¬
Ј¬ЎӯЈ¬![]() ЈЁ
ЈЁ![]() әНөгAІ»ЦШәПЈ©Ј®
әНөгAІ»ЦШәПЈ©Ј®
ўЩЗу![]() өДіӨЈ®
өДіӨЈ®
ўЪЗу![]() өДіӨЈ®
өДіӨЈ®
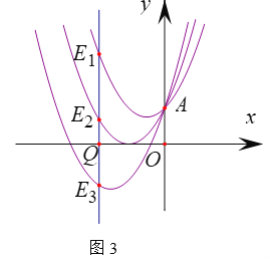
ЈЁ2Ј©ИзНј2Ј¬өгPҙУөгAіц·ўЈ¬СШyЦбПтЙПФЛ¶ҜЈ¬№эөгPЧчyЦбөДҙ№ПЯЈ¬Ҫ»ЕЧОпПЯ![]() УЪөг
УЪөг![]() Ј¬
Ј¬![]() Ј¬Ҫ»ЕЧОпПЯ
Ј¬Ҫ»ЕЧОпПЯ![]() УЪөг
УЪөг![]() Ј¬
Ј¬![]() Ј¬Ҫ»ЕЧОпПЯ
Ј¬Ҫ»ЕЧОпПЯ![]() УЪөг
УЪөг![]() Ј¬
Ј¬![]() Ј¬ЎӯЎӯЈ¬Ҫ»ЕЧОпПЯ
Ј¬ЎӯЎӯЈ¬Ҫ»ЕЧОпПЯ![]() УЪөг
УЪөг![]() Ј¬
Ј¬![]() ЈЁ
ЈЁ![]() ФЪөЪ¶юПуПЮЈ©Ј®
ФЪөЪ¶юПуПЮЈ©Ј®
ўЩЗу![]() өДЦөЈ®
өДЦөЈ®
ўЪЗу![]() өДЦөЈ®
өДЦөЈ®
ЈЁ3Ј©№эxЦбЙПөДөгQЈЁФӯөгіэНвЈ©Ј¬ЧчxЦбөДҙ№ПЯ·ЦұрҪ»ЕЧОпПЯ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬ЎӯЈ¬
Ј¬ЎӯЈ¬![]() УЪөг
УЪөг![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬ЎӯЈ¬
Ј¬ЎӯЈ¬![]() Ј¬КЗ·сҙжФЪПЯ¶О
Ј¬КЗ·сҙжФЪПЯ¶О![]() ЈЁiЈ¬jОӘХэХыКэЈ©Ј¬К№
ЈЁiЈ¬jОӘХэХыКэЈ©Ј¬К№![]() Ј¬ИфҙжФЪЈ¬ЗуіцiЈ«jөДЧоРЎЦөЈ»ИфІ»ҙжФЪЈ¬ЛөГчАнУЙЈ®
Ј¬ИфҙжФЪЈ¬ЗуіцiЈ«jөДЧоРЎЦөЈ»ИфІ»ҙжФЪЈ¬ЛөГчАнУЙЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ЕЧОпПЯ![]() Ҫ»xЦбУЪ
Ҫ»xЦбУЪ![]() Ј¬
Ј¬![]() БҪөгЈ¬УлyЦбҪ»УЪөгCЈ¬ACЈ¬BCЈ®MОӘПЯ¶ОOBЙПөДТ»ёц¶ҜөгЈ¬№эөгMЧч
БҪөгЈ¬УлyЦбҪ»УЪөгCЈ¬ACЈ¬BCЈ®MОӘПЯ¶ОOBЙПөДТ»ёц¶ҜөгЈ¬№эөгMЧч![]() ЦбЈ¬Ҫ»ЕЧОпПЯУЪөгPЈ¬Ҫ»BCУЪөгQЈ®
ЦбЈ¬Ҫ»ЕЧОпПЯУЪөгPЈ¬Ҫ»BCУЪөгQЈ®
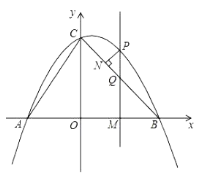
ЈЁ1Ј©ЗуЕЧОпПЯөДұнҙпКҪЈ»
ЈЁ2Ј©№эөгPЧч![]() Ј¬ҙ№ЧгОӘөгNЈ®ЙиMөгөДЧшұкОӘ
Ј¬ҙ№ЧгОӘөгNЈ®ЙиMөгөДЧшұкОӘ![]() Ј¬ЗлУГә¬mөДҙъКэКҪұнКҫПЯ¶ОPNөДіӨЈ¬ІўЗуіцөұmОӘәОЦөКұPNУРЧоҙуЦөЈ¬ЧоҙуЦөКЗ¶аЙЩЈҝ
Ј¬ЗлУГә¬mөДҙъКэКҪұнКҫПЯ¶ОPNөДіӨЈ¬ІўЗуіцөұmОӘәОЦөКұPNУРЧоҙуЦөЈ¬ЧоҙуЦөКЗ¶аЙЩЈҝ
ЈЁ3Ј©КФМҪҫҝөгMФЪФЛ¶Ҝ№эіМЦРЈ¬КЗ·сҙжФЪХвСщөДөгQЈ¬К№өГТФAЈ¬CЈ¬QОӘ¶ҘөгөДИэҪЗРОКЗөИСьИэҪЗРОЈ®ИфҙжФЪЈ¬ЗлЗуіцҙЛКұөгQөДЧшұкЈ»ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
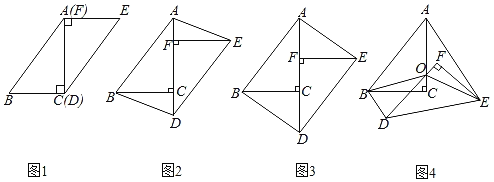
ЎҫМвДҝЎҝФЪТ»ҙОКэС§СРҫҝРФС§П°ЦРЈ¬РЎұшҪ«БҪёцИ«өИөДЦұҪЗИэҪЗРОЦҪЖ¬ABCәНDEFЖҙФЪТ»ЖрЈ¬К№өгAУлөгFЦШәПЈ¬өгCУлөгDЦШәПЈЁИзНј1Ј©Ј¬ЖдЦРЎПACBЈҪЎПDFEЈҪ90ЎгЈ¬BCЈҪEFЈҪ3cmЈ¬ACЈҪDFЈҪ4cmЈ¬ІўҪшРРИзПВСРҫҝ»о¶ҜЈ®
»о¶ҜТ»ЈәҪ«Нј1ЦРөДЦҪЖ¬DEFСШAC·ҪПтЖҪТЖЈ¬Б¬ҪбAEЈ¬BDЈЁИзНј2Ј©Ј¬өұөгFУлөгCЦШәПКұНЈЦ№ЖҪТЖЈ®
ЈЁЛјҝјЈ©Нј2ЦРөДЛДұЯРОABDEКЗЖҪРРЛДұЯРОВрЈҝЗлЛөГчАнУЙЈ®
ЈЁ·ўПЦЈ©өұЦҪЖ¬DEFЖҪТЖөҪДіТ»О»ЦГКұЈ¬РЎұш·ўПЦЛДұЯРОABDEОӘҫШРОЈЁИзНј3Ј©Ј®ЗуAFөДіӨЈ®
»о¶Ҝ¶юЈәФЪНј3ЦРЈ¬ИЎADөДЦРөгOЈ¬ФЩҪ«ЦҪЖ¬DEFИЖөгOЛіКұХл·ҪПтРэЧӘҰБ¶ИЈЁ0ЎЬҰБЎЬ90Ј©Ј¬Б¬ҪбOBЈ¬OEЈЁИзНј4Ј©Ј®
ЈЁМҪҫҝЈ©өұEFЖҪ·ЦЎПAEOКұЈ¬МҪҫҝOFУлBDөДКэБҝ№ШПөЈ¬ІўЛөГчАнУЙЈ®
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com