
【题目】有![]() 、
、![]() 、
、![]() 三家工厂依次坐落在一条笔直的公路边,甲、乙两辆运货卡车分别从
三家工厂依次坐落在一条笔直的公路边,甲、乙两辆运货卡车分别从![]() 、
、![]() 工厂同时出发,沿公路匀速驶向
工厂同时出发,沿公路匀速驶向![]() 工厂,最终到达
工厂,最终到达![]() 工厂,设甲、乙两辆卡车行驶
工厂,设甲、乙两辆卡车行驶![]() 后,与
后,与![]() 工厂的距离分别为
工厂的距离分别为![]() 、
、![]() (
(![]() ).
).![]() 、
、![]() 与
与![]() 函数关系如图所示,根据图象解答下列问题.(提示:图中较粗的折线表示的是
函数关系如图所示,根据图象解答下列问题.(提示:图中较粗的折线表示的是![]() 与
与![]() 的函数关系.)
的函数关系.)
(![]() )
)![]() 、
、![]() 两家工厂之间的距离为__________
两家工厂之间的距离为__________ ![]() ,
, ![]() __________,
__________, ![]() 点坐标是__________.
点坐标是__________.
(![]() )求甲、乙两车之间的距离不超过
)求甲、乙两车之间的距离不超过![]() 时,
时, ![]() 的取值范围.
的取值范围.

【答案】(1)见解析;(2)![]() 或
或![]() .
.
【解析】试题分析:(1)根据y轴的最大距离为B、C两地间的距离,再加上A、B两地间的距离即可;先求出甲的速度,再求出到达C地的时间,然后加上0.5即为a的值;利用待定系数法求一次函数解析式求出甲从B地到C地的函数解析式,再求出乙的解析式,然后联立求解即可得到点P的坐标;
(2)根据两函数解析式列出不等式组求解即可.
试题解析:解:(1)由图可知,A、B两地相距30km,B、C两地相距90km,所以,A、C两家工厂之间的距离为30+90=120km,甲的速度为:30÷0.5=60km/h,90÷60=1.5小时,∴a=0.5+1.5=2;
设甲:0.5≤x≤2时的函数解析式为y=kx+b,∵函数图象经过点(0.5,0)、(2,90),∴![]() ,解得:
,解得: ![]() ,∴y=60x﹣30,乙的速度为90÷3=30km/h,乙函数解析式为:y=30x,联立
,∴y=60x﹣30,乙的速度为90÷3=30km/h,乙函数解析式为:y=30x,联立![]() ,解得:
,解得: ![]() ,所以,点P(1,30);
,所以,点P(1,30);
故答案为:120,2,(1,30);
(2)∵甲、乙两车之间的距离不超过10km,∴ ![]() ,解不等式①得,x≥
,解不等式①得,x≥![]() ,解不等式②得,x≤
,解不等式②得,x≤![]() ,所以,x的取值范围是
,所以,x的取值范围是![]() ≤x≤
≤x≤![]() ;
;
当甲车停止后,乙行驶![]() 小时时,两车相距10km,故
小时时,两车相距10km,故![]() ≤x≤3时,甲、乙两车之间的距离不超过10km.
≤x≤3时,甲、乙两车之间的距离不超过10km.
综上所述:x的取值范围是![]() ≤x≤
≤x≤![]() 或
或![]() ≤x≤3甲、乙两车之间的距离不超过10km.
≤x≤3甲、乙两车之间的距离不超过10km.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD⊥BC于点D,BE平分∠ABC,若∠ABC=64°,∠AEB=70°.
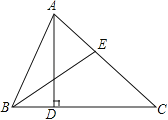
(1)求∠CAD的度数;
(2)若点F为线段BC上的任意一点,当△EFC为直角三角形时,求∠BEF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
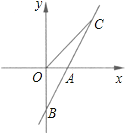
【题目】如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,﹣2).
(1)求直线AB的解析式;
(2)若直线AB上的点C在第一象限,且S△BOC=2,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.一个游戏的中奖概率是![]() ,则做10次这样的游戏一定会中奖
,则做10次这样的游戏一定会中奖
B.为了解全国中学生的心理健康情况,应该采用普查的方式
C.一组数据6,8,7,8,8,9,10的众数和中位数都是8
D.若甲组数据的方差S2甲=0.01,乙组数据的方差S2乙=0.1,则乙组数据比甲组数据稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD和四边形![]() 位似,位似比
位似,位似比![]() =2,四边形A′B′C′D′和四边形
=2,四边形A′B′C′D′和四边形![]() 位似,位似比
位似,位似比![]() =1.四边形
=1.四边形![]() 和四边形ABCD是位似图形吗?位似比是多少?
和四边形ABCD是位似图形吗?位似比是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列事件发生的概率,把A,B,C,D填入事件后的括号里.
A.发生的概率为0 B.发生的概率小于![]()
C.发生的概率大于![]() D.发生的概率为1
D.发生的概率为1
(1)从一副扑克牌中任意抽取一张,是红桃;( )
(2)2024年2月有29天;( )
(3)小波能举起500 kg的大石头;( )
(4)从5张分别写有数字1,2,4,6,8的卡片中任取一张,卡片上数字恰为偶数.( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,坐标原点O为矩形ABCD的对称中心,顶点A的坐标为(1,t),AB∥x轴,矩形A′B′C′D′与矩形ABCD是位似图形,点O为位似中心,点A′,B′分别是点A,B的对应点,![]() .已知关于x,y的二元一次方程
.已知关于x,y的二元一次方程![]() (m,n是实数)无解,在以m,n为坐标(记为(m,n)的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则kt的值等于( )
(m,n是实数)无解,在以m,n为坐标(记为(m,n)的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则kt的值等于( )

A.![]() B.1 C.
B.1 C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一不透明的布袋里,装有红、黄、蓝三种颜色的小球(除颜色外其余都相同),其中有红球2个,蓝球1个,黄球若干个,现从中任意摸出一个球是红球的概率为![]()
(1)求口袋中黄球的个数;
(2)甲同学先随机摸出一个小球(不放回),再随机摸出一个小球,请用“树状图法”或“列表法”,求两次摸出都是红球的概率;
(3)现规定:摸到红球得5分,摸到黄球得3分,摸到蓝球得2分(每次摸后放回),乙同学在一次摸球游戏中,第一次随机摸到一个红球第二次又随机摸到一个蓝球,若随机再摸一次,求乙同学三次摸球所得分数之和不低于10分的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com