
【题目】已知四边形ABCD是边长为2的菱形,∠BAD=60°,对角线AC与BD交于点O,过点O的直线EF交AD于点E,交BC于点F. 
(1)求证:△AOE≌△COF;
(2)若∠EOD=30°,求CE的长.
【答案】
(1)证明:∵四边形ABCD是菱形,
∴AO=CO,AD∥BC,
∴∠OAE=∠OCF,
在△AOE和△COF中, 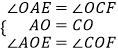 ,
,
∴△AOE≌△COF(ASA);
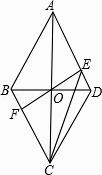
(2)解:∵∠BAD=60°,
∴∠DAO= ![]() ∠BAD=
∠BAD= ![]() ×60°=30°,
×60°=30°,
∵∠EOD=30°,
∴∠AOE=90°﹣30°=60°,
∴∠AEF=180°﹣∠DAO﹣∠AOE=180°﹣30°﹣60°=90°,
∵菱形的边长为2,∠DAO=30°,
∴OD= ![]() AD=
AD= ![]() ×2=1,
×2=1,
∴AO= ![]() =
= ![]() =
= ![]() ,
,
∴AE=CF= ![]() ×
× ![]() =
= ![]() ,
,
∵菱形的边长为2,∠BAD=60°,
∴高EF=2× ![]() =
= ![]() ,
,
在Rt△CEF中,CE= ![]() =
= ![]() =
= ![]() .
.
【解析】(1)根据菱形的对角线互相平分可得AO=CO,对边平行可得AD∥BC,再利用两直线平行,内错角相等可得∠OAE=∠OCF,然后利用“角边角”证明△AOE和△COF全等;(2)根据菱形的对角线平分一组对角求出∠DAO=30°,然后求出∠AEF=90°,然后求出AO的长,再求出EF的长,然后在Rt△CEF中,利用勾股定理列式计算即可得解.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=﹣ ![]() x+1与x轴、y轴分别交于B点、A点,直线y=2x﹣2与x轴、y轴分别交于D点、E点,两条直线交于点C;
x+1与x轴、y轴分别交于B点、A点,直线y=2x﹣2与x轴、y轴分别交于D点、E点,两条直线交于点C;
(1)求A、B、C、D、E的坐标;
(2)请用相似三角形的相关知识证明:AB⊥DE;
(3)求△CBD的外接圆的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,池塘边有一块长为18米,宽为10米的长方形土地,现在将其中三面留出宽都是x米的小路,中间余下的长方形部分做菜地.
(1)菜地的长a = 米,宽b= 米(用含x的代数式表示);
(2)菜地的面积S= 平方米(用含x的代数式表示);
(3)当x=1米时,求菜地的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲、乙两个不透明的布袋里,都装有3个大小、材质完全相同的小球,其中甲袋中的小球上分别标有数字0,1,2;乙袋中的小球上分别标有数字﹣1,﹣2,0.现从甲袋中任意摸出一个小球,记其标有的数字为x,再从乙袋中任意摸出一个小球,记其标有的数字为y,以此确定点M的坐标(x,y).
(1)请你用画树状图或列表的方法,写出点M所有可能的坐标;
(2)求点M(x,y)在函数y=﹣ ![]() 的图象上的概率.
的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
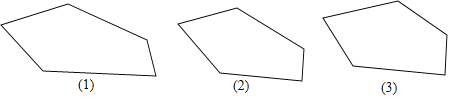
【题目】如图是一个多边形,你能否用一直线去截这个多边形,使得到的新多边形分别满足下列条件:![]() 画出图形,把截去的部分打上阴影
画出图形,把截去的部分打上阴影![]()
![]() 新多边形内角和比原多边形的内角和增加了
新多边形内角和比原多边形的内角和增加了![]() .
.
![]() 新多边形的内角和与原多边形的内角和相等.
新多边形的内角和与原多边形的内角和相等.
![]() 新多边形的内角和比原多边形的内角和减少了
新多边形的内角和比原多边形的内角和减少了![]() .
.
![]() 将多边形只截去一个角,截后形成的多边形的内角和为
将多边形只截去一个角,截后形成的多边形的内角和为![]() ,求原多边形的边数.
,求原多边形的边数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一透明的敞口正方体容器ABCD﹣A′B′C′D′装有一些液体,棱AB始终在水平桌面上,容器底部的倾斜角为α(∠CBE=α,如图1所示).探究 如图1,液面刚好过棱CD,并与棱BB′交于点Q,此时液体的形状为直三棱柱,其三视图及尺寸如图2所示.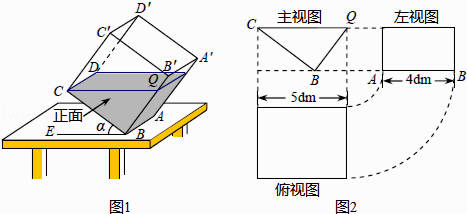
解决问题:
(1)CQ与BE的位置关系是 , BQ的长是dm;
(2)求液体的体积;(参考算法:直棱柱体积V液=底面积S△BCQ×高AB)
(3)求α的度数.(注:sin49°=cos41°= ![]() ,tan37°=
,tan37°= ![]() )
)
(4)延伸:在图4的基础上,于容器底部正中间位置,嵌入一平行于侧面的长方形隔板(厚度忽略不计),得到图5,隔板高NM=1dm,BM=CM,NM⊥BC.继续向右缓慢旋转,当α=60°时,通过计算,判断溢出容器的液体能否达到4dm3 . 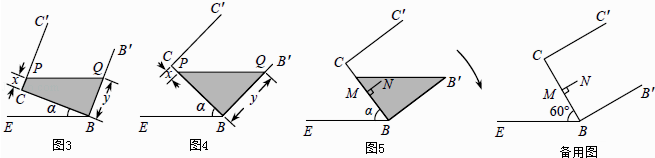
查看答案和解析>>
科目:初中数学 来源: 题型:
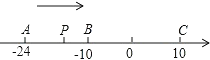
【题目】已知数轴上有A,B,C三个点,分别表示有理数﹣24,﹣10,10,动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒.
(1)用含t的代数式表示P到点A和点C的距离:
PA=________,PC=________;
(2)当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,Q点到达C点后,再立即以同样的速度返回,运动到终点A.在点Q开始运动后,P,Q两点之间的距离能否为2个单位?如果能,请求出此时点P表示的数;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四张背面完全相同的纸牌A、B、C、D中,其中正面分别画有四个不同的几何图形(如图),小华将这4张纸牌背面朝上洗匀后摸出一张(不放回),再从余下的3张纸牌中摸出一张.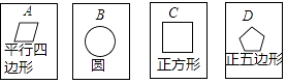
(1)用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌可用A、B、C、D表示);
(2)求摸出两张纸牌牌面上所画几何图形,既是轴对称图形又是中心对称图形的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com