【题目】如图，池塘边有一块长为18米，宽为10米的长方形土地，现在将其中三面留出宽都是x米的小路，中间余下的长方形部分做菜地.
（1）菜地的长a = 米，宽b= 米（用含x的代数式表示）；
（2）菜地的面积S= 平方米（用含x的代数式表示）；
（3）当x=1米时，求菜地的面积．
【答案】（1）18﹣2x，10﹣x；（2）（18﹣2x）（10﹣x）；（3）144m2.
【解析】
本题可先根据所给的图形，得出菜地的长和宽，然后根据长方形面积公式求出面积；第三问可以直接将x=1代入第二问所求的面积式子中，得出结果．
解：（1）∵其余三面留出宽都是x米的小路，
∴由图可以看出：菜地的长为18-2x米，宽为10-x米；
（2）由（1）知：菜地的长为18-2x米，宽为10-x米，
所以菜地的面积为S=（18-2x）（10-x）；
（3）由（2）得菜地的面积为：S=（18-2x）（10-x），
当x=1时，S=（18-2）（10-1）=144m2．
故答案分别为：（1）18﹣2x，10﹣x；（2）（18﹣2x）（10﹣x）；（3）144m2.
科目：初中数学 来源： 题型：
【题目】 “囧”（jiong）是近时期网络流行语，像一个人脸郁闷的神情．如图所示，一张边长为20的正方形的纸片，剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案（阴影部分）．设剪去的小长方形长和宽分别为x、y，剪去的两个小直角三角形的两直角边长也分别为x、y．
（1）用含有x、y的代数式表示右图中“囧”的面积；
（2）当
时，求此时“囧”的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为节约用水、保护水资源，本市制定了一套节约用水的管理措施，其中规定每月用水量超过m（吨）时，超过部分每吨加收环境保护费 
元．下图反映了每月收取的水费y（元）与每月用水量x（吨）之间的函数关系的图象．按上述方案，一家酒店四、五两月用水量及缴费情况如表：
月份 | 用水量x（吨） | 水费y（元） |
四月 | 35 | 59.5 |
五月 | 80 | 151 |
（1）求出m的值；
（2）写出y与x之间的函数关系式，并指出自变量x的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】按照有关规定：距离铁轨道200米以内的区域内不宜临路新建学校、医院、敬老院和集中住宅区等噪声敏感建筑物．
如图是一个小区平面示意图，矩形ABEF为一新建小区，直线MN为高铁轨道，C、D是直线MN上的两点，点C、A、B在一直线上，且DA⊥CA，∠ACD=30°．小王看中了①号楼A单元的一套住宅，与售楼人员的对话如下：
（1）小王心中一算，发现售楼人员的话不可信，请你通过计算用所学的数学知识说明理由．
（2）若一列长度为228米的高铁以70米/秒的速度通过时，则A单元用户受到影响时间有多长？（ 温馨提示：
≈1.4，
≈1.7，
≈6.1）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】计算：
（1）3ab2（﹣
a2b）2abc；
（2）（﹣
x2y）3（﹣3xy2）；
（3）（﹣3xy2）3（
x3y）；
（4）（x2+3x）﹣2（4x﹣x2）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知四边形ABCD是边长为2的菱形，∠BAD=60°，对角线AC与BD交于点O，过点O的直线EF交AD于点E，交BC于点F． 
（1）求证：△AOE≌△COF；
（2）若∠EOD=30°，求CE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，□ABCD中∠ABC=90°，AB=4cm，BC=8cm，AC的垂直平分线EF分别交AD、BC于点E、F，垂足为O．
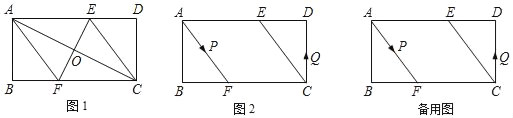
（1）如图1，连接AF、CE．求证：四边形AFCE为平行四边形．
（2）如图1，求AF的长．
（3）如图2，动点P、Q分别从A、C两点同时出发，沿△AFB和△CDE各边匀速运动一周．即点P自A→F→B→A停止，点Q自C→D→E→C停止．在运动过程中，点P的速度为每秒1cm，点Q的速度为每秒0.8cm，设运动时间为t秒，若当A、P、C、Q四点为顶点的四边形是平行四边形时，求t的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】问题一：如图1，已知AC=160km，甲，乙两人分别从相距30km的A，B两地同时出发到C地，若甲的速度为80km/h，乙的速度为60km/h，设乙行驶时间为x（h）, 两车之间距离为y（km）.
(1)当甲追上乙时，x=_________.
(2)请用x的代数式表示y.
问题二：如图2，若将上述线段AC弯曲后视作钟表外围的一部分，线段AB正好对应钟表上的弧AB（1小时的间隔），易知∠AOB=30°.
(1)分针OD指向圆周上的点的速度为每分钟转动_______km；时针OE指向圆周上的点的速度为每分钟转动_______km.
(2)若从2:00起计时，求几分钟后分针与时针第一次重合？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
