
【题目】计算:(1)-2-(-3)+(-8); (2)(-16)÷![]() ×(-
×(-![]() );
);
(3)![]() ; (4)
; (4)![]() ;
;
(5)![]()
【答案】(1)﹣7;(2)20;(3)﹣332;(4)3![]() ;(5)﹣50.
;(5)﹣50.
【解析】
(1)直接按照有理数的混合运算进行;
(2)直接按照有理数的混合运算进行;
(3)按照有理数混合运算的顺序,先乘除后加减;
(4)按照有理数混合运算的顺序,先乘方后乘除最后算加减;
(5)先算乘除,再算加减.
(1)-2-(-3)+(-8)
=﹣2+3﹣8
=﹣7;
(﹣16)÷![]() ×(﹣
×(﹣![]() )
)
=(﹣16)×![]() ×(﹣
×(﹣![]() )
)
=20;
(3)(﹣110)×3+8÷(﹣4)
=﹣330﹣2
=﹣332;
(4)(﹣4)×(﹣3)+(﹣![]() )﹣23
)﹣23
=12﹣![]() ﹣8
﹣8
=3![]() ;
;
(5)25×0.5﹣(﹣50)÷4+25×(﹣3)
=12.5+12.5﹣75
=﹣50.


科目:初中数学 来源: 题型:
【题目】如图,从热气球C处测得地面A、B两点的俯角分别是30°、45°,如果此时热气球C处的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是( )
A.200米
B.200 ![]() 米
米
C.220 ![]() 米
米
D.100( ![]() +1)米
+1)米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙两人到距离A地35千米的B地办事,甲步行先走,乙骑车后走,两人行进的路程和时间的关系如图所示,根据图示提供的信息解答:
(1)乙比甲晚 小时出发;乙出发 小时后追上甲;
(2)求乙比甲早几小时到达B地?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=﹣ ![]() x+1与x轴、y轴分别交于B点、A点,直线y=2x﹣2与x轴、y轴分别交于D点、E点,两条直线交于点C;
x+1与x轴、y轴分别交于B点、A点,直线y=2x﹣2与x轴、y轴分别交于D点、E点,两条直线交于点C;
(1)求A、B、C、D、E的坐标;
(2)请用相似三角形的相关知识证明:AB⊥DE;
(3)求△CBD的外接圆的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上一点,
上一点,![]() 是
是![]() 延长线上一点,且
延长线上一点,且![]() .
.
(1)在图1中,求证:![]() .
.
(2)在图1中,若点![]() 在
在![]() 上且
上且![]() ,试猜想
,试猜想![]() 、
、![]() 、
、![]() 之间的数量关系并证明.
之间的数量关系并证明.
(3)运用(1)(2)解答中所积累的经验知识,完成下题:如图2,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 在
在![]() 上,
上,![]() ,且
,且![]() ,若
,若![]() ,求
,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,池塘边有一块长为18米,宽为10米的长方形土地,现在将其中三面留出宽都是x米的小路,中间余下的长方形部分做菜地.
(1)菜地的长a = 米,宽b= 米(用含x的代数式表示);
(2)菜地的面积S= 平方米(用含x的代数式表示);
(3)当x=1米时,求菜地的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲、乙两个不透明的布袋里,都装有3个大小、材质完全相同的小球,其中甲袋中的小球上分别标有数字0,1,2;乙袋中的小球上分别标有数字﹣1,﹣2,0.现从甲袋中任意摸出一个小球,记其标有的数字为x,再从乙袋中任意摸出一个小球,记其标有的数字为y,以此确定点M的坐标(x,y).
(1)请你用画树状图或列表的方法,写出点M所有可能的坐标;
(2)求点M(x,y)在函数y=﹣ ![]() 的图象上的概率.
的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一透明的敞口正方体容器ABCD﹣A′B′C′D′装有一些液体,棱AB始终在水平桌面上,容器底部的倾斜角为α(∠CBE=α,如图1所示).探究 如图1,液面刚好过棱CD,并与棱BB′交于点Q,此时液体的形状为直三棱柱,其三视图及尺寸如图2所示.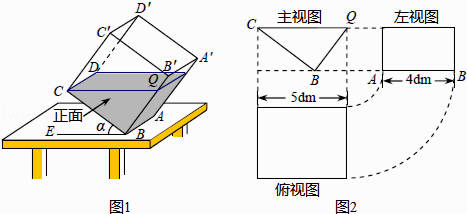
解决问题:
(1)CQ与BE的位置关系是 , BQ的长是dm;
(2)求液体的体积;(参考算法:直棱柱体积V液=底面积S△BCQ×高AB)
(3)求α的度数.(注:sin49°=cos41°= ![]() ,tan37°=
,tan37°= ![]() )
)
(4)延伸:在图4的基础上,于容器底部正中间位置,嵌入一平行于侧面的长方形隔板(厚度忽略不计),得到图5,隔板高NM=1dm,BM=CM,NM⊥BC.继续向右缓慢旋转,当α=60°时,通过计算,判断溢出容器的液体能否达到4dm3 . 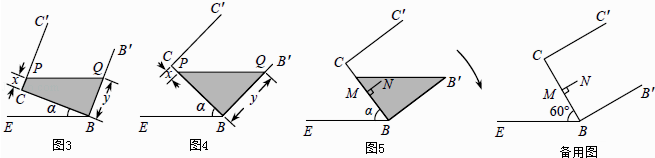
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】华联超市购进一批四阶魔方,按进价提高40%后标价,为了让利于民,增加销量,超市决定打八折出售,这时每个魔方的售价为28元.
(1)求魔方的进价?
(2)超市卖出一半后,正好赶上双十一促销,商店决定将剩下的魔方以每3个80元的价格出售,很快销售一空,这批魔方超市共获利2800元,求该超市共购进魔方多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com