
【题目】已知,□ABCD中∠ABC=90°,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
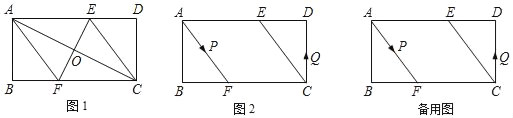
(1)如图1,连接AF、CE.求证:四边形AFCE为平行四边形.
(2)如图1,求AF的长.
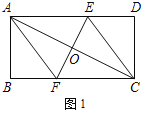
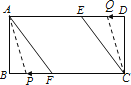
(3)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,点P的速度为每秒1cm,点Q的速度为每秒0.8cm,设运动时间为t秒,若当A、P、C、Q四点为顶点的四边形是平行四边形时,求t的值.
【答案】(1)证明见解析;(2)AF=5;(3)以A,C,P,Q四点为顶点的四边形是平行四边形时,t=![]() 秒.
秒.
【解析】分析:(1)①先证明四边形ABCD为平行四边形,再根据对角线互相垂直平分的平行四边形是菱形作出判定;
②根据勾股定理即可求AF的长;
(2)分情况讨论可知,P点在BF上,Q点在ED上时,才能构成平行四边形,根据平行四边形的性质列出方程求解即可;
详解:(1)∵四边形ABCD是矩形,
∴AD∥BC,
∴∠CAD=∠ACB,∠AEF=∠CFE.
∵EF垂直平分AC,
∴OA=OC.
在△AOE和△COF中,
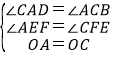 ,
,
∴△AOE≌△COF(AAS),
∴OE=OF(AAS).
∵EF⊥AC,
∴四边形AFCE为菱形.即四边形AFCE为平行四边形.
②设菱形的边长AF=CF=xcm,则BF=(8-x)cm,
在Rt△ABF中,AB=4cm,由勾股定理,得
16+(8-x)2=x2,
解得:x=5,
∴AF=5.
(2)由作图可以知道,P点AF上时,Q点CD上,此时A,C,P,Q四点不可能构成平行四边形;
同理P点AB上时,Q点DE或CE上,也不能构成平行四边形.
∴只有当P点在BF上,Q点在ED上时,才能构成平行四边形,
∴以A,C,P,Q四点为顶点的四边形是平行四边形时,
∴PC=QA,
∵点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,
∴PC=t,QA=12-0.8t,
∴t=12-0.8t,
解得:t=![]() .
.
∴以A,C,P,Q四点为顶点的四边形是平行四边形时,t=![]() 秒.
秒.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,直线y=x向下平移2个单位后和直线y=kx+b(k≠0)重合,直线y=kx+b(k≠0)与x轴交于点A,与y轴交于点B .
(1)请直接写出直线y=kx+b(k≠0)的表达式和点B的坐标;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,池塘边有一块长为18米,宽为10米的长方形土地,现在将其中三面留出宽都是x米的小路,中间余下的长方形部分做菜地.
(1)菜地的长a = 米,宽b= 米(用含x的代数式表示);
(2)菜地的面积S= 平方米(用含x的代数式表示);
(3)当x=1米时,求菜地的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
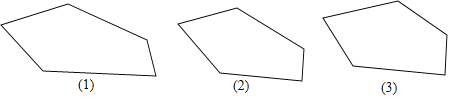
【题目】如图是一个多边形,你能否用一直线去截这个多边形,使得到的新多边形分别满足下列条件:![]() 画出图形,把截去的部分打上阴影
画出图形,把截去的部分打上阴影![]()
![]() 新多边形内角和比原多边形的内角和增加了
新多边形内角和比原多边形的内角和增加了![]() .
.
![]() 新多边形的内角和与原多边形的内角和相等.
新多边形的内角和与原多边形的内角和相等.
![]() 新多边形的内角和比原多边形的内角和减少了
新多边形的内角和比原多边形的内角和减少了![]() .
.
![]() 将多边形只截去一个角,截后形成的多边形的内角和为
将多边形只截去一个角,截后形成的多边形的内角和为![]() ,求原多边形的边数.
,求原多边形的边数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一透明的敞口正方体容器ABCD﹣A′B′C′D′装有一些液体,棱AB始终在水平桌面上,容器底部的倾斜角为α(∠CBE=α,如图1所示).探究 如图1,液面刚好过棱CD,并与棱BB′交于点Q,此时液体的形状为直三棱柱,其三视图及尺寸如图2所示.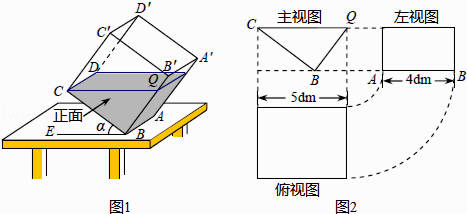
解决问题:
(1)CQ与BE的位置关系是 , BQ的长是dm;
(2)求液体的体积;(参考算法:直棱柱体积V液=底面积S△BCQ×高AB)
(3)求α的度数.(注:sin49°=cos41°= ![]() ,tan37°=
,tan37°= ![]() )
)
(4)延伸:在图4的基础上,于容器底部正中间位置,嵌入一平行于侧面的长方形隔板(厚度忽略不计),得到图5,隔板高NM=1dm,BM=CM,NM⊥BC.继续向右缓慢旋转,当α=60°时,通过计算,判断溢出容器的液体能否达到4dm3 . 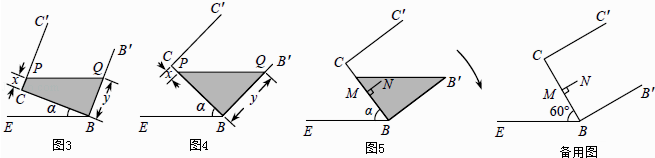
查看答案和解析>>
科目:初中数学 来源: 题型:
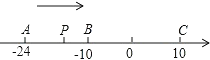
【题目】已知数轴上有A,B,C三个点,分别表示有理数﹣24,﹣10,10,动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒.
(1)用含t的代数式表示P到点A和点C的距离:
PA=________,PC=________;
(2)当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,Q点到达C点后,再立即以同样的速度返回,运动到终点A.在点Q开始运动后,P,Q两点之间的距离能否为2个单位?如果能,请求出此时点P表示的数;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知平行四边形ABCD,对角线AC,BD相交于点O,∠OBC=∠OCB.
(1)求证:平行四边形ABCD是矩形;
(2)请添加一个条件使矩形ABCD为正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富少年儿童的业余生活,某社区要在如图中的AB所在的直线上建一图书室,本社区有两所学校所在的位置在点C和点D处,CA⊥AB于A,DB⊥AB于B.已知AB=2.5km,CA=1.5km,DB=1.Okm,试问:图书室E应该建在距点A多少km处,才能使它到两所学校的距离相等?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com