
【题目】如图,数轴上A,B两点对应的数分别-4,8.有一动点P从点A出发第一次向左运动1个单位长度;然后在新的位置第二次运动,向右运动2个单位长度;在此位置第三次运动,向左运动3个单位长度,…按照如此规律不断地左右运动
![]()
(1)当运动到第2018次时,求点P所对应的有理数.
(2)点P会不会在某次运动时恰好到达某一个位置,使点P到点B的距离是点P到点A的距离的3倍?若可能请求出此时点P的位置,若不可能请说明理由.
【答案】(1)1005;(2)点P运动了第11次和第6次恰好到达这一位置,此时P的位置为-10和-1.
【解析】
(1)往右用加,往左用减,计算即可得出答案;
(2)分三种情况讨论:①当点P在点A左侧时;②当点P在点A和点B之间时;③当点P在点B的右侧时,再分别求出PA和PB所表示的代数式,根据PB=3PA计算,即可得出答案.
解:(1)依题意可得:-4-1+2-3+4-5+…-2017+2018=-4+1009=1005
答:当运动到第2018次时,点P所对应的有理数为1005;
(2)设点P对应的有理数的值为x
①当点P在点A左侧时,PA=-4-x,PB=8-x
依题意可得:8-x=3(-4-x)
解得:x=-10
②当点P在点A和点B之间时,PA=x-(-4)=x+4,PB=8-x
依题意可得:8-x=3(x+4)
解得:x=-1
③当点P在点B的右侧时,PA=x-(-4)=x+4,PB=x-8
依题意可得:x-8=3(x+4)
解得:x=-10,与点P在点B右侧矛盾,故舍去
∴-10和-1分别是点P运动了第11次和第6次到达的位置


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
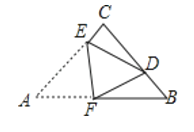
【题目】如图,在△ABC中, ![]() , AC=BC=3, 将△ABC折叠,使点A落在BC 边上的点D处,EF为折痕,若AE=2,则
, AC=BC=3, 将△ABC折叠,使点A落在BC 边上的点D处,EF为折痕,若AE=2,则![]() 的值为_____________.
的值为_____________.
【答案】![]()
【解析】分析:过点D作DG![]() AB于点G.根据折叠性质,可得AE=DE=2,AF=DF,CE=1,
AB于点G.根据折叠性质,可得AE=DE=2,AF=DF,CE=1,
在Rt△DCE中,由勾股定理求得![]() ,所以DB=
,所以DB=![]() ;在Rt△ABC中,由勾股定理得
;在Rt△ABC中,由勾股定理得![]() ;在Rt△DGB中,由锐角三角函数求得
;在Rt△DGB中,由锐角三角函数求得![]() ,
, ![]() ;
;
设AF=DF=x,则FG= ![]() ,在Rt△DFG中,根据勾股定理得方程
,在Rt△DFG中,根据勾股定理得方程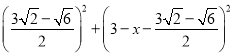 =
=![]() ,解得
,解得![]() ,从而求得
,从而求得![]() .的值
.的值
详解:
如图所示,过点D作DG![]() AB于点G.
AB于点G.

根据折叠性质,可知△AEF![]() △DEF,
△DEF,
∴AE=DE=2,AF=DF,CE=AC-AE=1,
在Rt△DCE中,由勾股定理得![]() ,
,
∴DB=![]() ;
;
在Rt△ABC中,由勾股定理得![]() ;
;
在Rt△DGB中, ![]() ,
, ![]() ;
;
设AF=DF=x,得FG=AB-AF-GB=![]() ,
,
在Rt△DFG中, ![]() ,
,
即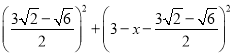 =
=![]() ,
,
解得![]() ,
,
∴![]() =
=![]() =
=![]() .
.
故答案为: ![]() .
.
点睛:主要考查了翻折变换的性质、勾股定理、锐角三件函数的定义;解题的关键是灵活运用折叠的性质、勾股定理、锐角三角函数的定义等知识来解决问题.
【题型】填空题
【结束】
18
【题目】规定:[x]表示不大于x 的最整数,(x) 表示不小于x的最小整数,[x) 表示最接近x的整数(x≠n+0.5,n为整数),例如:[2.3]=2,(2.3)=3,[2.3)=2,则下列说法正确的是__________(写出所有正确说法).
①当x=1.7时,[x]+(x)+[x)=6;
②当x=-2.1时,[x]+(x)+[x)=-7;
③方程4[x]+3(x)+[x)=11的解为1<x<1.5;
④当-1<x<1时, 函数y=[x]+(x)+x 的图像y=4x 的图像有两个交点.
查看答案和解析>>
科目:初中数学 来源: 题型:
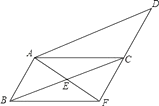
【题目】如图,在ABCD中,已知E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF.
(1)求证:AB=CF;
(2)当BC与AF满足什么数量关系时,四边形ABFC是矩形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(a ,2![]() )是直线y=
)是直线y=![]() x上一点,以A为圆心,2为半径作⊙A,若P(x,y)是第一象限内⊙A上任意一点,则
x上一点,以A为圆心,2为半径作⊙A,若P(x,y)是第一象限内⊙A上任意一点,则![]() 的最小值为( )
的最小值为( )
A. 1 B. ![]() C.
C. ![]() —1 D.
—1 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
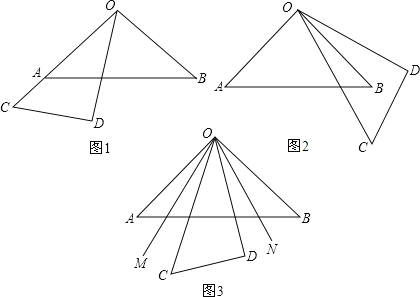
【题目】已知将一副三角板(直角三角板OAB和直角三角板OCD,∠AOB=90°,∠COD=30°)如图1摆放,点O、A、C在一条直线上.将直角三角板OCD绕点O逆时针方向转动,变化摆放如图位置
(1)如图1,当点O、A、C在同一条直线上时,则∠BOD的度数是多少?
(2)如图2,若要OB恰好平分∠COD,则∠AOC的度数是多少?
(3)如图3,当三角板OCD摆放在∠AOB内部时,作射线OM平分∠AOC,射线ON平分∠BOD,如果三角板OCD在∠AOB内绕点O任意转动,∠MON的度数是否发生变化?如果不变,求其值;如果变化,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有3张纸牌,分別是红桃3、红桃4和黑桃5(简称红3,红4,黑5).把牌洗匀后甲先抽取一张,记下花色和数字后将牌放回,洗匀后乙再抽取一张.
(1)两次抽得纸牌均为红桃的概率;(请用“画树状图”或“列表”等方法写出分析过程)
(2)甲、乙两人做游戏,现有两种方案.A方案:若两次抽得花色相同则甲胜,否则乙胜.B方案:若两次抽得纸牌的数字和为奇数则甲胜,否则乙胜.请问甲选择哪种方案胜率更高?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家商场同时出售同样的水瓶和水杯,且定价相同,请根据图中提供的信息,回答下列问题:
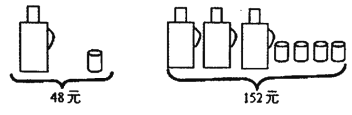
(1)一个水瓶与一个水杯分别是多少元?(请列方程解应用题)
(2)为了迎接新年,两家商场都在搞促销活动,甲商场规定:这两种商品都打八折;乙商场规定:买一个水瓶赠送两个水杯,另外购买的水杯按原价卖.若某单位想要买5个水瓶和12个水杯,请问选择哪家商场购买更合算,并说明理由(水瓶和水杯必须在同一家购买).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是由若干个完全相同的小正方体组成的一个几何体。
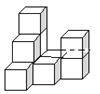
(1)图中有 块小正方体;
(2)请画出这个几何体的左视图和俯视图;(用阴影表示)
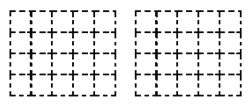
(3)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的俯视图和左视图不变,那么最多可以再添加几个小正方体?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自行车厂一周计划生产150辆自行车,平均每天生产辆,由于各种原因实际每天生产量与计划量相比有出入,下表是某周的生产情况(超产为正、减产为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 |
|
|
|
|
|
|
|
(1)根据记录可知前三天共生产 辆;
(2)产量最多的一天比生产量最少的一天多生产 辆;
(3)该厂实行计划工资制,每辆车![]() 元,超额完成任务每辆奖
元,超额完成任务每辆奖![]() 元,少生产一辆扣
元,少生产一辆扣![]() 元,那么该厂工人这一周的工资总额是多少?
元,那么该厂工人这一周的工资总额是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com