
【题目】甲、乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲、乙两人相距s(米),甲行走的时间为t(分),s关于t的函数图象的一部分如图所示. 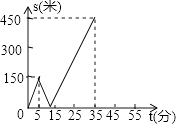
(1)求甲行走的速度;
(2)在坐标系中,补画s关于t的函数图象的其余部分;
(3)问甲、乙两人何时相距360米?
【答案】
(1)解:甲行走的速度:150÷5=30(米/分);
(2)解:当t=35时,甲行走的路程为:30×35=1050(米),乙行走的路程为:(35﹣5)×50=1500(米),
∴当t=35时,乙已经到达图书馆,甲距图书馆的路程还有(1500﹣1050)=450米,
∴甲到达图书馆还需时间;450÷30=15(分),
∴35+15=50(分),
∴当s=0时,横轴上对应的时间为50.
补画的图象如图所示(横轴上对应的时间为50),
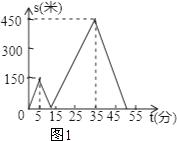
(3)解:如图2,
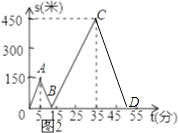
设乙出发经过x分和甲第一次相遇,根据题意得:150+30x=50x,
解得:x=7.5,
7.5+5=12.5(分),
由函数图象可知,当t=12.5时,s=0,
∴点B的坐标为(12.5,0),
当12.5≤t≤35时,设BC的解析式为:s=kt+b,(k≠0),
把C(35,450),B(12.5,0)代入可得: ![]()
解得: ![]() ,
,
∴s=20t﹣250,
当35<t≤50时,设CD的解析式为s=k1x+b1,(k1≠0),
把D(50,0),C(35,450)代入得: 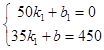
解得: 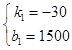
∴s=﹣30t+1500,
∵甲、乙两人相距360米,即s=360,
解得:t1=30.5,t2=38,
∴当甲行走30.5分钟或38分钟时,甲、乙两人相距360米.
【解析】(1)由图象可知t=5时,s=150米,根据速度=路程÷时间,即可解答;(2)根据图象提供的信息,可知当t=35时,乙已经到达图书馆,甲距图书馆的路程还有(1500﹣1050)=450米,甲到达图书馆还需时间;450÷30=15(分),所以35+15=50(分),所以当s=0时,横轴上对应的时间为50.(3)分别求出当12.5≤t≤35时和当35<t≤50时的函数解析式,根据甲、乙两人相距360米,即s=360,分别求出t的值即可.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
【题目】人数相等的甲、乙两班学生参加了同一次数学测验, 班级平均分和方差如下:平均分都为110,甲、乙两班方差分别为340、280,则成绩较为稳定的班级为( )
A. 甲班 B. 乙班 C. 两班成绩一样稳定 D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面各组数据能判断是直角三角形的是( )
A. 三边长都为2B. 三边长分别为2,3,2
C. 三边长分别为13,12,5D. 三边长分别为4,5,6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转运甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则李燕获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).
(1)请用列表或画树状图的方法表示出上述游戏中两数和的所有可能的结果;
(2)分别求出李燕和刘凯获胜的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E、F分别为边AB、CD的中点,BD是对角线,过点A作AG∥DB交CB的延长线于点G. 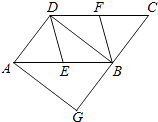
(1)求证:DE∥BF;
(2)若∠G=90°,求证:四边形DEBF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果从一个多边形的一个顶点出发作它的对角线,最多能将多边形分成2011个三角形,那么这个多边形是 ( )
A. 2012边形 B. 2013边形 C. 2014边形 D. 2015边形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com