
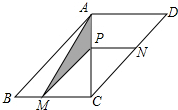
 如图,在平行四边形中,对角线AC⊥BC,AC=BC=2,动点P从点A出发沿AC向终点C移动,过点P分别作PM∥AB交BC于M,PN∥AD交DC于N.连结AM.
如图,在平行四边形中,对角线AC⊥BC,AC=BC=2,动点P从点A出发沿AC向终点C移动,过点P分别作PM∥AB交BC于M,PN∥AD交DC于N.连结AM.分析 (1)根据直角三角形的性质得出PM>CM,即可得出答案;
(2)求出△PM是等腰直角三角形,求出PC=CM=1,求出四边形PMCN是平行四边形,根据面积公式求出即可.
解答 解:(1)四边形PMCN不可能是菱形,
理由是:∵点P在运动过程中,△PCM始终是一个直角三角形,斜边PM大于直角边MC,
∴四边形PMCN不可能是菱形;
(2)∵AC=2,AP=1,
∴CP=1,
∵AC⊥BC,AC=BC=2,
∴∠BAC=45°,
∵PM∥AB,
∴∠CPM=∠BAC=45°,
∵AC⊥BC,
∴△CPM是等腰直角三角形,
∴CM=CP=1,
∵PM∥AB,PN∥AD,
∴四边形PMCN是平行四边形,
∴平行四边形PMCN的面积为CM×CP=1×1=1.
点评 本题考查了平行四边形的性质和判定,直角三角形的性质,等腰直角三角形的性质的应用,解此题的关键是求出△PCM是等腰直角三角形,难度适中.


科目:初中数学 来源: 题型:解答题
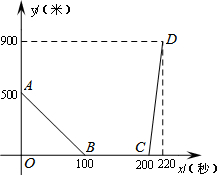 设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车向原地返回.设x秒后两车间的距离为y千米,y关于x的函数关系如图所示,
设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车向原地返回.设x秒后两车间的距离为y千米,y关于x的函数关系如图所示,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
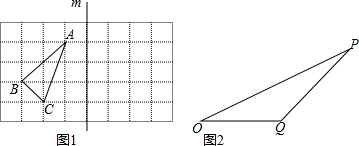
 如图,双曲线y=$\frac{k}{x}$(x>0)经过△OAB的顶点A和OB的中点C,AB∥x轴,点A的坐标为(2,3),△OAB的面积为9,则k=6.
如图,双曲线y=$\frac{k}{x}$(x>0)经过△OAB的顶点A和OB的中点C,AB∥x轴,点A的坐标为(2,3),△OAB的面积为9,则k=6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
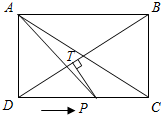 如图,在矩形ABCD中,AD=60cm,CD=80cm,连接AC、BD.动点P从点D出发,以5cm/s速度沿边DC匀速向点C运动,到达点C即停止,过点P作BD的垂线,垂足为T.设点P运动的时间为t s.
如图,在矩形ABCD中,AD=60cm,CD=80cm,连接AC、BD.动点P从点D出发,以5cm/s速度沿边DC匀速向点C运动,到达点C即停止,过点P作BD的垂线,垂足为T.设点P运动的时间为t s.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com