

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
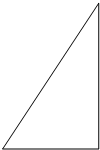 ����һ��ֱ�������α߽��ϣ�����ֱ�DZ߷ֱ�6cm��8cm��Ҫ���������߽��ϲü���һ��������������β��ϣ����������ü������������ε�����Ƕ��٣�ע�⣺Ҫ����Ŷ���Լ�������ĸ��
����һ��ֱ�������α߽��ϣ�����ֱ�DZ߷ֱ�6cm��8cm��Ҫ���������߽��ϲü���һ��������������β��ϣ����������ü������������ε�����Ƕ��٣�ע�⣺Ҫ����Ŷ���Լ�������ĸ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
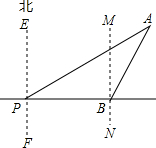 ��ͼ��һ���ִ�λ��Pʱ��ã�����A���䱱ƫ��60�㷽������������������ʻ400���ﵽ��B������ʱ��õ���A�ڱ�ƫ��30�㷽����֪�Ե���AΪԲ�ģ�350����Ϊ�뾶�ķ�Χ���а������ڣ���ͨ������ش��ִ��������У��Ƿ��д���Σ�գ�$��\sqrt{3}��1.7��$��
��ͼ��һ���ִ�λ��Pʱ��ã�����A���䱱ƫ��60�㷽������������������ʻ400���ﵽ��B������ʱ��õ���A�ڱ�ƫ��30�㷽����֪�Ե���AΪԲ�ģ�350����Ϊ�뾶�ķ�Χ���а������ڣ���ͨ������ش��ִ��������У��Ƿ��д���Σ�գ�$��\sqrt{3}��1.7��$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
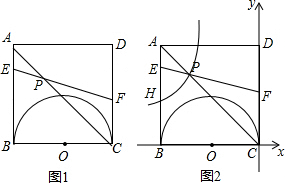
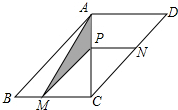 ��ͼ����ƽ���ı����У��Խ���AC��BC��AC=BC=2������P�ӵ�A������AC���յ�C�ƶ�������P�ֱ���PM��AB��BC��M��PN��AD��DC��N������AM��
��ͼ����ƽ���ı����У��Խ���AC��BC��AC=BC=2������P�ӵ�A������AC���յ�C�ƶ�������P�ֱ���PM��AB��BC��M��PN��AD��DC��N������AM���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 28097 | B�� | 28098 | C�� | 28077 | D�� | 28087 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
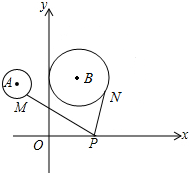 ��ͼ��ƽ��ֱ������ϵ�У��ֱ��Ե�A��-2��3����B��3��4��ΪԲ�ģ���1��3Ϊ�뾶����A����B��M��N�ֱ��ǡ�A����B�ϵĶ��㣬PΪx���ϵĶ��㣬��PM+PN����Сֵ����$\sqrt{74}$-4��
��ͼ��ƽ��ֱ������ϵ�У��ֱ��Ե�A��-2��3����B��3��4��ΪԲ�ģ���1��3Ϊ�뾶����A����B��M��N�ֱ��ǡ�A����B�ϵĶ��㣬PΪx���ϵĶ��㣬��PM+PN����Сֵ����$\sqrt{74}$-4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
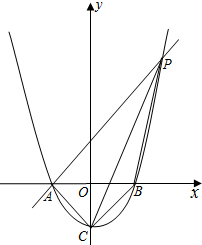 ��ͼ����֪������y=ax2+c��x���ڵ�A��-2��0���͵�B����y���ڵ�C��0��-2����
��ͼ����֪������y=ax2+c��x���ڵ�A��-2��0���͵�B����y���ڵ�C��0��-2�����鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com