
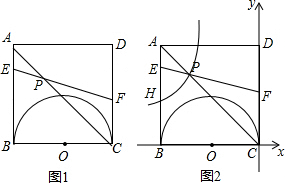
���� ��1���߶�EF��BCƽ��ʱ��AE=DF��2-t=2t-2���ⷽ�̾Ϳ��������tֵ��
��2����EF���ԲO����ʱ���������ߵ����ʣ�����������ͼ�����ù��ɶ��������߳������Ϳ��������t��ֵ��
��3����1��t��2ʱ����AEP�ס�CFP���Ϳ��������P��λ�ò��ᷢ���仯AP��PC=AE��CF�Ǹ���ֵΪ$\frac{1}{2}$����AB=BC=2�����ݹ��ɶ������$AC=2\sqrt{2}$�������ó�CP=$\frac{4}{3}\sqrt{2}$���Ӷ����P������Ϊ��$-\frac{4}{3}��\frac{4}{3}$�������ô���ϵ�����������˫���ߵĺ�����ϵʽ����x=-2����˫���ߵĹ�ϵʽ��y=$\frac{8}{9}$���Ӷ����H�����꣬�������꼴�����$\frac{BH}{AH}$��ֵ��
��� �⣺��1����E��F������t��ʱ��EF��BC��
��ʱBE=t��CF=4-2t��BE=CF����t=4-2t��
��$t=\frac{4}{3}$��
��2����ͼ����E��F������t��ʱ��EF���Բ���У���F����FK��BC����AB��K��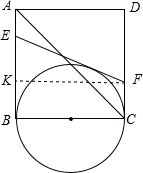 ��BE=t��CF=4-2t��EK=EB-KB=EB-FC=t-��4-2t��=3t-4��
��BE=t��CF=4-2t��EK=EB-KB=EB-FC=t-��4-2t��=3t-4��
EF=BE+CF�����߳���ȣ�=4-t
��Rt��EKF��EF2=EK2+KF2=��4-t��2=��3t-4��2+22
��ã�$t=\frac{{2+\sqrt{2}}}{2}$��$t=\frac{{2-\sqrt{2}}}{2}$��
��1��t��2����$t=\frac{{2+\sqrt{2}}}{2}$��
��3����1��t��2ʱ��
��ͼ����$\frac{AE}{CF}=\frac{2-t}{4-2t}=\frac{1}{2}$��
��AB��DC��
���APE�ס�CPE ��$\frac{AP}{PC}=\frac{AE}{CF}=\frac{1}{2}$��
����P��λ����t����ֵ�أ�
���P��λ�ò��ᷢ���仯��AP��PC��ֵΪ$\frac{1}{2}$��
��AB=BC=2��
��$AC=2\sqrt{2}$��
��AP��PC=1��2��
��CP=$\frac{4}{3}\sqrt{2}$��
��P��$-\frac{4}{3}��\frac{4}{3}$����
��P��$-\frac{4}{3}��\frac{4}{3}$������˫���߽���ʽ$y=\frac{k}{x}$����$k=-\frac{16}{9}$��
�෴���������Ľ���ʽΪ$y=-\frac{16}{9x}$��
��x=-2�����y=$\frac{8}{9}$��
��H��$-2��\frac{8}{9}$����
��$\frac{BH}{AH}=\frac{4}{5}$��
���� �����Ƿ������������ۺ��⣬���ߵ����ʣ����߳�������Ӧ�ã����ɶ�����Ӧ�ã�����ϵ�������������Ľ���ʽ�����������Ƶ��ж������ʣ�����������ͼ���ϵ�����������ȣ���һ�����Ѷȣ�


 Сѧ��ʱ��ѵϵ�д�
Сѧ��ʱ��ѵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����6��6�������������У�ÿ��С�����ε����������1���Ը��Ϊ���㣬��һ�����Ϊ13�������Σ�
��ͼ����6��6�������������У�ÿ��С�����ε����������1���Ը��Ϊ���㣬��һ�����Ϊ13�������Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪A��-4��n����B��2��-4����һ�κ���y=kx+b��ͼ��ͷ���������y=$\frac{m}{x}$��ͼ����������㣬��ʽkx+b-$\frac{m}{x}$��0�Ľ⼯Ϊ-4��x��0��x��2��
��ͼ����֪A��-4��n����B��2��-4����һ�κ���y=kx+b��ͼ��ͷ���������y=$\frac{m}{x}$��ͼ����������㣬��ʽkx+b-$\frac{m}{x}$��0�Ľ⼯Ϊ-4��x��0��x��2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com