
���� ����a��b��c��2a+3b+4c=0���жϳ�a��0�жϢ٣�����2a+3b+4c=��2a+c��+3b+3c��3a+3b+3c=3��a+b+c�������жϢڣ���������y=ax2+bx+c��x�ύ������Ϊ��x1��0������x2��0�������ǿ�֪x1+x2=-$\frac{b}{a}$��x1x2=$\frac{c}{a}$��2a+3b+4c=0�������õ���x1-x2��2=��x1+x2��2-4x1x2=$\frac{{b}^{2}}{{a}^{2}}-\frac{4c}{a}$=$\frac{{b}^{2}}{{a}^{2}}+\frac{3b}{a}+2$���ٸ���m��ֵ�������жϳ��Գ���ֱ�ߣ������жϢۣ������m��ֵ�����ǿɵ�$\frac{{b}^{2}}{{a}^{2}}+\frac{3b}{a}+2$=$\frac{1}{3}$���жϷ��̸�����������жϢܣ�
��� �⣺��a��b��c��2a+3b+4c=0��
��a��0���ٴ���
2a+3b+4c=��2a+c��+3b+3c
��a��c��
��2a+c��3a��
��2a+3b+4c=��2a+c��+3b+3c��3a+3b+3c=3��a+b+c������0��3��a+b+c����
��a+b+c��0������ȷ��
��������y=ax2+bx+c��x�ύ������Ϊ��x1��0������x2��0����
��������y=ax2+bx+c��x���Ͻصõ��߶γ�Ϊm��
��|x1-x2|=m��
��x1+x2=-$\frac{b}{a}$��x1x2=$\frac{c}{a}$��2a+3b+4c=0��
�ࣨx1-x2��2=��x1+x2��2-4x1x2=$\frac{{b}^{2}}{{a}^{2}}-\frac{4c}{a}$=$\frac{{b}^{2}}{{a}^{2}}+\frac{3b}{a}+2$��
��m=$\frac{2\sqrt{7}}{3}$ʱ��$\frac{{b}^{2}}{{a}^{2}}+\frac{3b}{a}+2=\frac{28}{9}$��
���$\frac{b}{a}=-\frac{10}{3}$��$\frac{b}{a}=\frac{1}{3}$��
��Գ���-$\frac{b}{2a}$=$\frac{5}{3}$��-$\frac{1}{6}$���۴���
��m������һ��ֵ�Ƿ���x2-$\frac{2}{3}$x+$\frac{1}{9}$=0�ĸ���
��m=$\frac{1}{3}$��
��$\frac{{b}^{2}}{{a}^{2}}+\frac{3b}{a}+2$=$\frac{1}{3}$��
����н⣬������ȷ��
������ȷ���Тڢܣ�
�ʴ�Ϊ�ڢܣ�
���� ������Ҫ��������������x�ύ���Լ����κ���ͼ����ϵ���Ĺ�ϵ��֪ʶ�������Ĺؼ����������ո���ϵ���Ĺ�ϵ���ر��Ǣ���Ҫ��$\frac{b}{a}$����һ�����壬������һ�����Ѷȣ�


 �»ƸԱ����ܾ�ϵ�д�
�»ƸԱ����ܾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
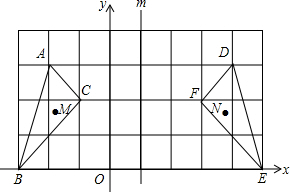 ��ͼ����ƽ��ֱ������ϵ�У���ABC���DEF����ֱ��m=1�Գƣ���M��N�ֱ����������������еĶ�Ӧ�㣬�����M�ĺ�������a����ô��N�ĺ������ǣ�������
��ͼ����ƽ��ֱ������ϵ�У���ABC���DEF����ֱ��m=1�Գƣ���M��N�ֱ����������������еĶ�Ӧ�㣬�����M�ĺ�������a����ô��N�ĺ������ǣ�������| A�� | -a | B�� | -a+1 | C�� | a+2 | D�� | -a+2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
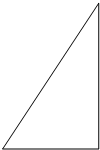 ����һ��ֱ�������α߽��ϣ�����ֱ�DZ߷ֱ�6cm��8cm��Ҫ���������߽��ϲü���һ��������������β��ϣ����������ü������������ε�����Ƕ��٣�ע�⣺Ҫ����Ŷ���Լ�������ĸ��
����һ��ֱ�������α߽��ϣ�����ֱ�DZ߷ֱ�6cm��8cm��Ҫ���������߽��ϲü���һ��������������β��ϣ����������ü������������ε�����Ƕ��٣�ע�⣺Ҫ����Ŷ���Լ�������ĸ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
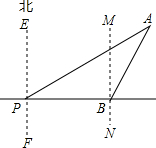 ��ͼ��һ���ִ�λ��Pʱ��ã�����A���䱱ƫ��60�㷽������������������ʻ400���ﵽ��B������ʱ��õ���A�ڱ�ƫ��30�㷽����֪�Ե���AΪԲ�ģ�350����Ϊ�뾶�ķ�Χ���а������ڣ���ͨ������ش��ִ��������У��Ƿ��д���Σ�գ�$��\sqrt{3}��1.7��$��
��ͼ��һ���ִ�λ��Pʱ��ã�����A���䱱ƫ��60�㷽������������������ʻ400���ﵽ��B������ʱ��õ���A�ڱ�ƫ��30�㷽����֪�Ե���AΪԲ�ģ�350����Ϊ�뾶�ķ�Χ���а������ڣ���ͨ������ش��ִ��������У��Ƿ��д���Σ�գ�$��\sqrt{3}��1.7��$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com