
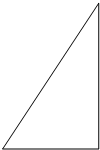
 现有一块直角三角形边角料,两条直角边分别长6cm和8cm,要你利用这块边角料裁剪出一个面积最大的正方形材料,你准备怎样裁剪?所得正方形的面积是多少?注意:要讨论哦,自己标上字母.
现有一块直角三角形边角料,两条直角边分别长6cm和8cm,要你利用这块边角料裁剪出一个面积最大的正方形材料,你准备怎样裁剪?所得正方形的面积是多少?注意:要讨论哦,自己标上字母. 分析 分类讨论:当正方形的两边在直角三角形的直角边上,如图1,AC=6cm,BC=8cm,四边形CDEF为正方形,设正方形的边长为xcm,则BD=BC-CD=8-x,证明△BED∽△BAC,利用相似比得到$\frac{x}{6}$=$\frac{8-x}{8}$,解得x=$\frac{24}{7}$;当正方形的一边在直角三角形的斜边上,如图2,AC=6cm,BC=8cm,四边形DEFG为正方形,作CN⊥AB于N,交DE于M,先利用勾股定理计算出AB=10,再利用面积法计算出CN=$\frac{24}{5}$,设正方形的边长为ycm,则DE=y,NM=DG=y,CM=CN-MN=$\frac{24}{5}$-y,接着证明△CED∽△CBA,利用相似比得到$\frac{\frac{24}{5}-y}{\frac{24}{5}}$=$\frac{y}{10}$,解得y=$\frac{120}{37}$,然后比较x和y的大小,然后可判断像(1)所示图形进行裁剪所得正方形的面积最大.
解答 解: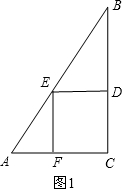 当正方形的两边在直角三角形的直角边上,如图1,AC=6cm,BC=8cm,四边形CDEF为正方形,
当正方形的两边在直角三角形的直角边上,如图1,AC=6cm,BC=8cm,四边形CDEF为正方形,
设正方形的边长为xcm,则BD=BC-CD=8-x,
∵DE∥AC,
∴△BED∽△BAC,
∴$\frac{DE}{AC}$=$\frac{BD}{BC}$,即$\frac{x}{6}$=$\frac{8-x}{8}$,解得x=$\frac{24}{7}$;
当正方形的一边在直角三角形的斜边上,如图2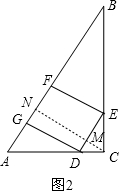 ,AC=6cm,BC=8cm,四边形DEFG为正方形,
,AC=6cm,BC=8cm,四边形DEFG为正方形,
作CN⊥AB于N,交DE于M,
在Rt△ABC中,AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=10,
∵$\frac{1}{2}$CN•AB=$\frac{1}{2}$CA•CB,
∴CN=$\frac{6×8}{10}$=$\frac{24}{5}$,
设正方形的边长为ycm,则DE=y,NM=DG=y,CM=CN-MN=$\frac{24}{5}$-y,
∵DE∥AB,
∴△CED∽△CBA,
∴$\frac{CM}{CN}$=$\frac{DE}{AB}$,即$\frac{\frac{24}{5}-y}{\frac{24}{5}}$=$\frac{y}{10}$,解得y=$\frac{120}{37}$,
∵$\frac{24}{7}$=$\frac{120}{35}$>$\frac{120}{37}$,
∴x>y,
∴当所裁正方形的两直角边在三角形的直角边上时,正方形的面积最大,最大值为($\frac{24}{7}$)2=$\frac{576}{49}$(cm2).
点评 本题考查了相似三角形的应用:利用影长测量物体的高度;利用相似测量河的宽度(测量距离);借助标杆或直尺测量物体的高度.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
 如图,当小明沿坡度i=1:3的坡面由A到B行走了100米,那么小明行走的水平距离AC=30$\sqrt{10}$米.(结果可以用根号表示).
如图,当小明沿坡度i=1:3的坡面由A到B行走了100米,那么小明行走的水平距离AC=30$\sqrt{10}$米.(结果可以用根号表示).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 所有正方形都全等 | |
| B. | 等腰梯形的对角线互相平分 | |
| C. | 相等的圆周角所对的弧相等 | |
| D. | 顺次连结四边形各边中点所得到的四边形是平行四边形 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,正方体的棱长为3,点M,N分别在CD,HE上,CM=$\frac{1}{2}$DM,HN=2NE,HC与NM的延长线交于点P,则tan∠NPH的值为( )
如图,正方体的棱长为3,点M,N分别在CD,HE上,CM=$\frac{1}{2}$DM,HN=2NE,HC与NM的延长线交于点P,则tan∠NPH的值为( )| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,双曲线y=$\frac{k}{x}$(x>0)经过△OAB的顶点A和OB的中点C,AB∥x轴,点A的坐标为(2,3),△OAB的面积为9,则k=6.
如图,双曲线y=$\frac{k}{x}$(x>0)经过△OAB的顶点A和OB的中点C,AB∥x轴,点A的坐标为(2,3),△OAB的面积为9,则k=6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com