Question

8．数学实验室：制作4张全等的直角三角形纸片（如图1），把这4张纸片拼成以弦长c为边长的正方形构成“弦图”（如图2），古代数学家利用“弦图”验证了勾股定理．

探索研究：
（1）小明将“弦图”中的2个三角形进行了旋转，得到图3，请利用图3证明勾股定理；
数学思考：
（2）小芳认为用其它的方法改变“弦图”中某些三角形的位置，也可以证明勾股定理．请你想一种方法支持她的观点（先在备用图中补全图形，再予以证明）．

Answer 1

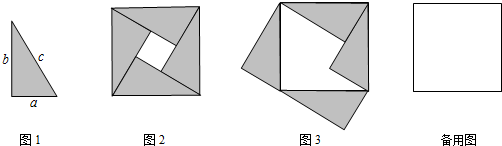
分析 （1）通过图形的面积的两种计算方法，即可得出结果；
（2）通过大正方形面积的两种计算方法，即可得出结果．

解答 解：（1）如图3所示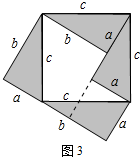
∵图形的面积表示为a²+b²+2×$\frac{1}{2}$ab=a²+b²+ab，
图形的面积也可表示为c²+4×$\frac{1}{2}$ab=c²+ab；
∴（a+b）²=c²+4×$\frac{1}{2}$ab，
a²+b²+ab=c²+ab，
∴a²+b²=c²
即直角三角形两直角边的平方和等于斜边的平方．
（2））如图4所示：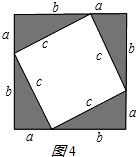
∵大正方形的面积表示为（a+b）²；
大正方形的面积也可表示为c²+4×$\frac{1}{2}$ab
∴（a+b）²=c²+4×$\frac{1}{2}$ab，
a²+b²+2ab=c²+2ab，
∴a²+b²=c²；
即直角三角形两直角边的平方和等于斜边的平方．

点评 此题考查了勾股定理的证明、正方形的性质、直角三角形面积的计算；关键是利用三角形和正方形边长的关系进行组合图形，利用面积的关系证明勾股定理．