
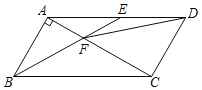
【题目】如图,在ABCD中,∠BAC=90°,∠ABC=60°,E是AD的中点,连结BE交对角线AC于点F,连结DF,则tan∠DFE的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
作![]() 交BE的延长线于G,作
交BE的延长线于G,作![]() 于H,由直角三角形的性质得出
于H,由直角三角形的性质得出![]() ,得出
,得出![]() ,证出
,证出![]() ,得出
,得出![]() ,得出
,得出![]() ,
,![]() ,
,![]() ,由直角三角形的性质得出
,由直角三角形的性质得出![]() ,
,![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,
,![]() ,由三角函数即可得出结果.
,由三角函数即可得出结果.
解:作DG⊥BE交BE的延长线于G,作FH⊥AD于H,如图所示:
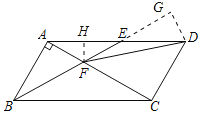
∵四边形ABCD是平行四边形,∠ABC=60°,
∴AD=BC,∠BAD=120°,
∵∠BAC=90°,∠ABC=60°,
∴∠ACB=30°,∠EAF=30°,
∴BC=2AB,
∵E是AD的中点,
∴AE=DE=AB,
∴∠AEB=30°=∠EAF,
∴AF=EF,
∵FH⊥AD,
∴AE=2EH,EF=2FH,![]() ,
,
∵∠DEG=∠AEB=30°,DG⊥BE,
∴DE=2DG,EG=![]() DG,
DG,
设DG=x,则EG=![]() x,AE=DE=2x,EF=
x,AE=DE=2x,EF=![]() ,
,
∴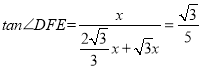 ;
;
故选:B.


 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
【题目】定义:有且仅有一组对角相等的凸四边形叫做“准平行四边形”.例如:凸四边形![]() 中,若
中,若![]() ,则称四边形
,则称四边形![]() 为准平行四边形.
为准平行四边形.
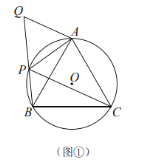
(1)如图①,![]() 是
是![]() 上的四个点,
上的四个点,![]() ,延长
,延长![]() 到
到![]() ,使
,使![]() .求证:四边形
.求证:四边形![]() 是准平行四边形;
是准平行四边形;
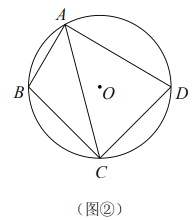
(2)如图②,准平行四边形![]() 内接于
内接于![]() ,
,![]() ,若
,若![]() 的半径为
的半径为![]() ,求
,求![]() 的长;
的长;
(3)如图③,在![]() 中,
中,![]() ,若四边形
,若四边形![]() 是准平行四边形,且
是准平行四边形,且![]() ,请直接写出
,请直接写出![]() 长的最大值.
长的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数 y=ax2+bx+c 的图象与 x 轴的交点的横坐标分别为-1,3,则:
①ac<0;②2a+b=0;③4a+2b+c>0;④对于任意 x 均有 ax2+bx≥a+b,其中结论正确的个数有( )
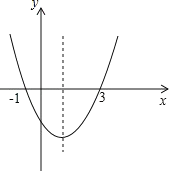
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
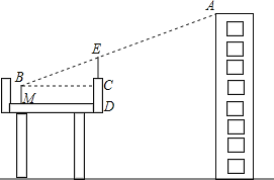
【题目】为了减轻二环高架上汽车的噪音污染,成都市政府计划在高架上的一些路段的护栏上方增加隔音屏.如图,工程人员在高架上的车道M处测得某居民楼顶的仰角∠ABC的度数是20°,仪器BM的高是0.8m,点M到护栏的距离MD的长为11m,求需要安装的隔音屏的顶部到桥面的距离ED的长(结果保留到0.1m,参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
查看答案和解析>>
科目:初中数学 来源: 题型:
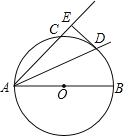
【题目】如图,AB为⊙O的直径,AC为⊙O的弦,AD平分∠BAC,交⊙O于点D,DE⊥AC,交AC的延长线于点E.
(1)求证:直线DE是⊙O的切线;
(2)若AE=8,⊙O的半径为5,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
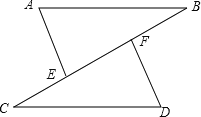
【题目】如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:BE=CF.
(2)若AB=CF,∠B=40°,求∠D的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的部分图象如图,则下列说法:①abc>0;②b+2a=0;③b2>4ac;④a+b+c<﹣3,正确的是( )
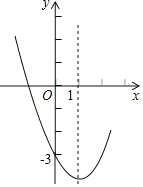
A.①②B.①②③C.①②④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若m、n(m<n)是关于x的方程1﹣(x﹣a)(x﹣b)=0的两根,且a<b,则a、b、m、n的大小关系是( ).
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程:x2﹣(m﹣3)x﹣m=0.
(1)试判断原方程根的情况;
(2)若抛物线y=x2﹣(m﹣3)x﹣m与x轴交于A(x1,0),B(x2,0)两点,则A,B两点间的距离是否存在最大或最小值?若存在,求出这个值;若不存在,请说明理由.
(友情提示:AB=|x2﹣x1|)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com