
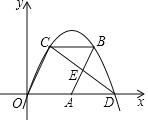
����Ŀ����ͼ�٣�������y=a(x2+2x-3)(a��0)��x�ύ�ڵ�A�͵�B����y�ύ�ڵ�C����OC=OB.
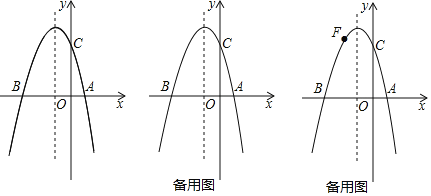
(1)ֱ��д����B��������( �� )�����������ߵĽ���ʽ��
(2)���D�������ߵĶ��㣬�����ߵĶԳ�����ֱ��l������BD���߶�OC�ϵĵ�E����ֱ��l�ĶԳƵ�E'ǡ�����߶�BD�ϣ����E�����ꣻ
(3)����FΪ�����ߵڶ�����ͼ���ϵ�һ�����㣬����BF��CF������BCF������ǡ�ABC�����һ��ʱ�����ʱ��F������.
���𰸡�(1)-3��0��y=-x2-2x+3��(2)��0��2����(3)��-2��3����-1��4��
��������
��1���ⷽ��a��x2+2x-3��=0�ɵ�B��-3��0����A��1��0������C��0��-3a����������OB=OC�õ�-3a=3�����a=-1���Ӷ��õ������߽���ʽ��
��2����ͼ�ڣ���һ��ʽ�䷽�õ�y=-��x+1��2+4����D��-1��4�������ô���ϵ�������ֱ��BD�Ľ���ʽΪy=2x+6����E��0��t�������öԳƵ����ʵ�E����-2��t����Ȼ���E����-2��t������y=2x+6���t���Ӷ��õ���E�����ꣻ
��3����ֱ��BC�Ľ���ʽΪy=x+3����FG��y�ύֱ��BC��G����ͼ�ۣ���F��x��-x2-2x+3����-3��x��0������G��x��x+3��������FG=-x2-3x�����������������ʽ�õ�S��FBC=![]() ��3����-x2-3x����Ȼ��������BCF���������ABC�����һ��õ�
��3����-x2-3x����Ȼ��������BCF���������ABC�����һ��õ�![]() ��3����-x2-3x��=
��3����-x2-3x��=![]() ��
��![]() ��4��3��Ȼ��ⷽ�����x�Ӷ��õ�F������꣮
��4��3��Ȼ��ⷽ�����x�Ӷ��õ�F������꣮
��1����y=0ʱ��a��x2+2x-3��=0�����x1=-3��x2=1����B��-3��0����A��1��0����
��x=0ʱ��y=-3a����C��0��-3a����
��OB=OC��
��-3a=3�����a=-1��
�������߽���ʽΪy=-x2-2x+3��
�ʴ�Ϊ-3��0��
��2����ͼ��
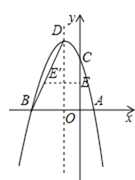
��y=-x2-2x+3=-��x+1��2+4��
��D��-1��4����
��ֱ��BD�Ľ���ʽΪy=kx+b��
��B��-3��0������-1��4�������![]() �����
�����![]() ��
��
��ֱ��BD�Ľ���ʽΪy=2x+6��
��E��0��t����
��E�������E����ֱ��x=-1�Գƣ�
��E����-2��t����
��E����-2��t������y=2x+6��t=-4+6=2��
���E��������0��2����
��3����ֱ��BC�Ľ���ʽΪy=x+3����FG��y�ύֱ��BC��G����ͼ��
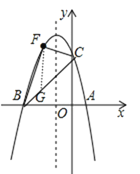
��F��x��-x2-2x+3����-3��x��0������G��x��x+3����
��FG=-x2-2x+3-��x+3��=-x2-3x��
��S��FBC=![]() ��3����-x2-3x����
��3����-x2-3x����
�ߡ�BCF���������ABC�����һ�룬
��![]() ��3����-x2-3x��=
��3����-x2-3x��=![]() ��
��![]() ��4��3�����x1=-1��x2=-2��
��4��3�����x1=-1��x2=-2��
��F���������-2��3����-1��4����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
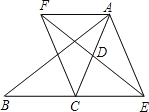
����Ŀ����֪����ͼ���ڡ�ABC�У�D��AC���е㣬E���߶�BC�ӳ�����һ�㣬����A��BE��ƽ�������߶�ED���ӳ��߽��ڵ�F������AE��CF��
��1����֤��AF��CE��
��2����AC��EF�����ж��ı���AFCE��ʲô�����ı��Σ���֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
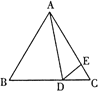
����Ŀ����ͼ���ڵȱ���ABC�У�DΪBC����һ�㣬EΪAC����һ�㣬�� ��ADE=60�㣬BD=4��CE=![]() ������ABC����� Ϊ��������
������ABC����� ��������
A. ![]() B. 15 C.
B. 15 C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
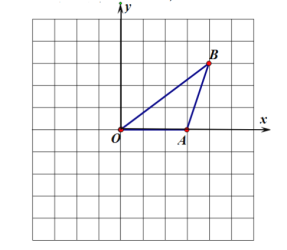
����Ŀ����ͼ����10��10�������У��ᡢ�������Ϊ�����ĵ������㣬����A��3,0����B��4,3�����Ǹ�㡣����AOB�Ƶ�O˳ʱ����ת90���õ���COD����A,B�Ķ�Ӧ��ֱ�Ϊ��C ��D����
��1��������COD����д�����и�������꣺C������������D������������
��2�������̶ȵ�ֱ����һ���E��ʹ��EB��AB����������E��λ�ã�
��3�������̶ȵ�ֱ����OB����һ��F��ʹ�á�OAF=45��(������������M��λ��)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() �ϲ��ֵ�ĺ�����
�ϲ��ֵ�ĺ�����![]() ��������
��������![]() �Ķ�Ӧֵ���±���
�Ķ�Ӧֵ���±���
| �� |
|
|
|
|
| �� |
| �� |
|
|
|
|
| �� |
![]() �����ϱ���գ�
�����ϱ���գ�
����������![]() ��Ľ���������________��________��
��Ľ���������________��________��
�������߾�����![]() ,________
,________![]() ��
��
���ڶԳ����Ҳ࣬![]() ��
��![]() �����________��
�����________��
![]() ��ȷ��������
��ȷ��������![]() �Ľ���ʽ��
�Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ���x2��4(k��1)x��4k2��0������ʵ����x1��x2
(1) ��k��ȡֵ��Χ
(2) ��x1x2��2|x1��x2|��4����k��ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�E��F�ֱ�Ϊ��AB��CD���е㣬����DE��BF����AB=2AD=4��
��1����֤����AED�ա�CFB��
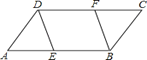
��2�����ı���DEBFΪ����ʱ����������ε������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
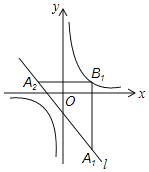
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���ֱ֪��l��y����x��1��˫����y��![]() ����l��ȡһ��A1����A1��x��Ĵ��߽�˫�����ڵ�B1����B1��y��Ĵ��߽�l�ڵ�A2�������������̽������A2��x��Ĵ��߽�˫�����ڵ�B2����B2��y��Ĵ��߽�l�ڵ�A3�������������εõ�l�ϵĵ�A1��A2��A3������An�����ǵ�An�ĺ�����Ϊan����a1��2����a2018��_____����Ҫ�������������εؽ�����ȥ����a1������ȡ��ֵ��_____��
����l��ȡһ��A1����A1��x��Ĵ��߽�˫�����ڵ�B1����B1��y��Ĵ��߽�l�ڵ�A2�������������̽������A2��x��Ĵ��߽�˫�����ڵ�B2����B2��y��Ĵ��߽�l�ڵ�A3�������������εõ�l�ϵĵ�A1��A2��A3������An�����ǵ�An�ĺ�����Ϊan����a1��2����a2018��_____����Ҫ�������������εؽ�����ȥ����a1������ȡ��ֵ��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AΪx����һ�㣬��B������Ϊ��a��b������OA��ABΪ�߹���OABC������O��C��B����������x�ύ�ڵ�D������CD������AB�ڵ�E����AE��BE�����C�ĺ�����Ϊ��������
A.a��bB.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com