
【题目】下列图形都是由同样大小的菱形按照一定规律组成的,请根据排列规律完成下列问题:
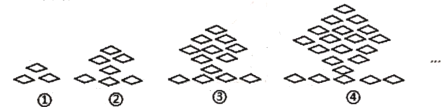
(1)填写下表:
图形序号 | 菱形个数(个) |
① | 3 |
② | 7 |
③ | ________ |
④ | ________ |
…… | …… |
(2)根据表中规律猜想,图n中菱形的个数_______(用含n的式子表示);
(3)是否存在一个图形恰好由111个菱形组成?若存在,求出图的序号;若不存在,说明理由.
【答案】(1)③ 13,④ 21;(2)图n中菱形的个数![]() (3)存在,是图⑩.
(3)存在,是图⑩.
【解析】
(1)观察图形,数出图③、图④中菱形的个数;
(2)设图n中菱形的个数为an(n为正整数),观察图形,找出部分图形中菱形的个数,根据菱形个数的变化(分成上下两部分,根据两部分的变化)可找出变化规律“an=n2+n+1(n为正整数)”;
(3)由(2)的结论结合菱形的个数为111,即可得出关于n的一元二次方程,解之取其正值(正整数值)即可得出结论.
(1)观察图形,可知:图③中有13个菱形,图④中有21个菱形.
故答案为:13;21.
(2)设图n中菱形的个数为an(n为正整数),
观察图形,可知:a1=3=1+2,a2=7=4+3,a3=13=9+4,a4=21=16+5,…,
∴an=n2+n+1(n为正整数).
(3)依题意,得:n2+n+1=111,
解得:n1=-11(舍去),a2=10,
∴存在一个图形恰好由111个菱形组成,该图形的序号为⑩.


科目:初中数学 来源: 题型:
【题目】某家具商场计划购进某种餐桌、餐椅进行销售,有关信息如表:
原进价(元/张) | 零售价(元/张) | 成套售价(元/套) | |
餐桌 | a | 270 | 500元 |
餐椅 | a﹣110 | 70 |
已知用600元购进的餐桌数量与用160元购进的餐椅数量相同.
(1)求表中a的值;
(2)若该商场购进餐椅的数量是餐桌数量的5倍还多20张,且餐桌和餐椅的总数量不超过200张.该商场计划将一半的餐桌成套(一张餐桌和四张餐椅配成一套)销售,其余餐桌、餐椅以零售方式销售.请问怎样进货,才能获得最大利润?最大利润是多少?
(3)由于原材料价格上涨,每张餐桌和餐椅的进价都上涨了10元,但销售价格保持不变.商场购进了餐桌和餐椅共200张,应怎样安排成套销售的销售量(至少10套以上),使得实际全部售出后,最大利润与(2)中相同?请求出进货方案和销售方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知已知抛物线经过原点O和x轴上一点A(4,0),抛物线顶点为E,它的对称轴与x轴交于点D,直线y=﹣2x﹣1经过抛物线上一点B(﹣2,m)且与y轴交于点C,与抛物线的对称轴交于点F.
(1)求m的值及该抛物线的解析式
(2)P(x,y)是抛物线上的一点,若S△ADP=S△ADC,求出所有符合条件的点P的坐标.
(3)点Q是平面内任意一点,点M从点F出发,沿对称轴向上以每秒1个单位长度的速度匀速运动,设点M的运动时间为t秒,是否能使以Q、A、E、M四点为顶点的四边形是菱形?若能,请直接写出点M的运动时间t的值;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)经过点A(1,-1)、B(3,3),且当1≤x≤3时,-1≤y≤3,则a的取值范围是___________
查看答案和解析>>
科目:初中数学 来源: 题型:
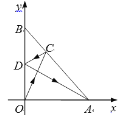
【题目】如图,一束光线从点O射出,照在经过A(1,0)、B(0,1)的镜面上的点C,经AB反射后,又照到竖立在y轴位置的镜面上的D点,最后经y轴再反射的光线恰好经过点A,则点C的坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中, ![]() ,点
,点![]() 到
到![]() 两边的距离相等,且
两边的距离相等,且![]() .
.
(1)先用尺规作出符合要求的点![]() (保留作图痕迹,不需要写作法),然后判断△ABP的形状,并说明理由;
(保留作图痕迹,不需要写作法),然后判断△ABP的形状,并说明理由;
(2)设![]() ,
,![]() ,试用
,试用![]() 、
、![]() 的代数式表示
的代数式表示![]() 的周长和面积;
的周长和面积;
(3)设![]() 与
与![]() 交于点
交于点![]() ,试探索当边
,试探索当边![]() 、
、![]() 的长度变化时,
的长度变化时,![]() 的值是否发生变化,若不变,试求出这个不变的值,若变化,试说明理由.
的值是否发生变化,若不变,试求出这个不变的值,若变化,试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 在平面直角坐标系中,有两条抛物线关于x轴对称,且它们的顶点相距6个单位长度,若其中一条抛物线的函数表达式为y=﹣x2+4x+2m,则m的值是( )
A.![]() B.
B.![]() C.1D.
C.1D.![]() 或
或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D,连接BD,CD,过点D作PD∥BC与AB的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)求证:BD2=PBAC.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com