
ЁОЬтФПЁПФГаЁбЇПЊеЙ4жжПЮЭтаЫШЄаЁзщЛюЖЏЃЌЗжБ№ЮЊAЃЛЛцЛЃКBЃЛЛњЦїШЫЃКCЃЛЬјЮшЃКDЃЛМЊЫћЃЎУПИібЇЩњЖМвЊбЁШЁвЛИіаЫШЄаЁзщВЮгыЛюЖЏЃЌаЁУїЖдЭЌбЇУЧбЁШЁЕФЛюЖЏаЮЪННјааСЫЫцЛњГщбљЕїВщЃЌИљОнЕїВщЭГМЦНсЙћЃЌЛцжЦСЫШчЯТЕФЭГМЦЭМЃК
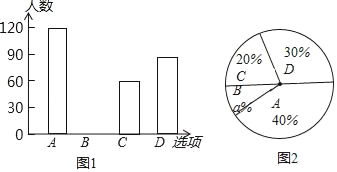
ЃЈ1ЃЉБОДЮЕїВщбЇЩњЙВЁЁ ЁЁШЫЃЌa=ЁЁ ЁЁЃЌВЂНЋЬѕаЮЭМВЙГфЭъећЃЛ
ЃЈ2ЃЉШчЙћИУаЃгабЇЩњ500ШЫЃЌдђбЁдёЁАЛњЦїШЫЁБЛюЖЏЕФбЇЩњЙРМЦгаЖрЩйШЫЃП
ЃЈ3ЃЉбЇаЃШУУПАрЭЌбЇдкAЃЌBЃЌCЃЌDЫФжжЛюЖЏаЮЪНжаЃЌЫцЛњГщШЁСНжжПЊеЙЛюЖЏЃЌЧыгУЪїзДЭМЛђСаБэЗЈЕФЗНЗЈЃЌЧѓУПАрГщШЁЕФСНжжаЮЪНЧЁКУЪЧЁАЛцЛЁБКЭЁАЛњЦїШЫЁБЕФИХТЪЃЎ
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЈ2ЃЉ50ШЫЃЈ3ЃЉ![]()
ЁОНтЮіЁПЃЈ1ЃЉИљОнЭГМЦЭМжаAРрШЫЪ§гыЫќЫљеМЕФАйЗжБШПЩЕУЕНЕїВщЕФзмШЫЪ§ЃЌИљОнАйЗжБШжЎКЭЮЊ1ПЩЕУaЕФжЕЃЌШЛКѓгУзмШЫЪ§ЗжБ№МѕШЅAЁЂCЁЂDРрЕФШЫЪ§ЕУЕНBРрШЫЪ§ЃЌдйВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ2ЃЉзмШЫЪ§ГЫвдбљБОжаBЕФАйЗжБШПЩЕУЃЛ
ЃЈ3ЃЉЛЪїзДЭМеЙЪОЫљга12жжЕШПЩФмЕФНсЙћЪ§ЃЌдйевГіФГАрЫљГщЕНЕФСНЯюЗНЪНЧЁКУЪЧЁАЛцЛЁБКЭЁАЛњЦїШЫЁБЕФНсЙћЪ§ЃЌШЛКѓИљОнИХТЪЙЋЪНЧѓНтЃЎ
(1)БОДЮЕїВщЕФбЇЩњШЫЪ§ЮЊ120ЁТ40%=300(ШЫ)ЃЌ
a%=140%30%20%=10%ЃЌ
Ёрa=10ЃЌ
BРрБ№ШЫЪ§ЮЊ300ЁС10%=30ЃЌ
ВЙШЋЭМаЮШчЯТЃК
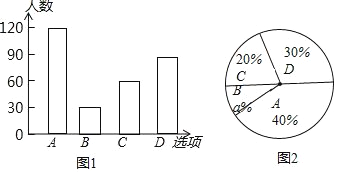
(2)500ЁС10=50(ШЫ)ЃЌ
Д№ЃКбЁдёЁАЛњЦїШЫЁБЛюЖЏЕФбЇЩњЙРМЦга50ШЫЃЛ
(3)ЛЪїзДЭМЮЊЃК
ЙВга12жжЕШПЩФмЕФНсЙћЪ§ЃЌЦфжаФГАрЫљГщЕНЕФСНЯюЗНЪНЧЁКУЪЧЁАЛцЛЁБКЭЁАЛњЦїШЫЁБЕФНсЙћЪ§ЮЊ2ЃЌ
ЫљвдФГАрЫљГщЕНЕФСНЯюЗНЪНЧЁКУЪЧЁАЛцЛЁБКЭЁАЛњЦїШЫЁБЕФИХТЪ![]()



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЕШбќжБНЧ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌНЋ
ЕФжаЕуЃЌНЋ![]() елЕўЃЌЪЙЕу
елЕўЃЌЪЙЕу![]() гыЕу
гыЕу![]() жиКЯЃЌ
жиКЯЃЌ![]() ЮЊелКлЃЌдђ
ЮЊелКлЃЌдђ![]() ЕФжЕЪЧЃЈ ЃЉ
ЕФжЕЪЧЃЈ ЃЉ
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЕиЕФвЛжжТЬЩЋЪпВЫ,дкЪаГЁЩЯШєжБНгЯњЪл,УПЖжРћШѓЮЊ1000дЊ,ОДжМгЙЄКѓЯњЪл,УПЖжРћШѓ4000дЊ,ООЋМгЙЄКѓЯњЪл, УПЖжРћШѓЮЊ7000дЊ.ЕБЕивЛМвЙЋЫОЯжгаетжжЪпВЫ140Жж,ИУЙЋЫОМгЙЄГЇЕФЩњВњФмСІЪЧ:ШчЙћЖдЪпВЫНјааДжМгЙЄ,УПЬьПЩМгЙЄ16Жж, ШчЙћЖдЪпВЫНјааОЋМгЙЄ,УПЬьПЩМгЙЄ6Жж,ЕЋУПЬьСНжжЗНЪНВЛФмЭЌЪБНјаа.ЪмМОНкЕШЬѕМўЕФЯожЦ,БиаыгУ15ЬьЪБМфНЋетХњЪпВЫШЋВПЯњЪлЛђМгЙЄЭъБЯ.ЮЊДЫ,ЙЋЫОбажЦСЫШ§жжЗНАИ:
ЗНАИ1:НЋЪпВЫШЋВПНјааДжМгЙЄ;
ЗНАИ2:ОЁПЩФмЕиЖдЪпВЫНјааОЋМгЙЄ,УЛРДЕУМАМгЙЄЕФЪпВЫ,дкЪаГЁЩЯжБНгГіЪл;
ЗНАИ3:НЋвЛВПЗжЪпВЫНјааОЋМгЙЄ, ЦфгрЪпВЫНјааДжМгЙЄ,ВЂИеКУ15ЬьЭъГЩ.
ШчЙћФуЪЧЙЋЫООРэ,ФуЛсбЁдёФФвЛжжЗНАИ? ЧыЭЈЙ§МЦЫуЫЕУї.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПAЮЊЁбCЩЯвЛЕуЃЌЙ§ЕуAзїЯвABЃЌШЁЯвABЩЯвЛЕуPЃЌШєТњзу![]() Ём
Ём![]() <1ЃЌдђГЦPЮЊЕуAЙигкЁбCЕФЛЦН№ЕуЃЎвбжЊЁбCЕФАыОЖЮЊ3ЃЌЕуAЕФзјБъЮЊЃЈ1ЃЌ0ЃЉЃЎ
<1ЃЌдђГЦPЮЊЕуAЙигкЁбCЕФЛЦН№ЕуЃЎвбжЊЁбCЕФАыОЖЮЊ3ЃЌЕуAЕФзјБъЮЊЃЈ1ЃЌ0ЃЉЃЎ
(1)ЕБЕуCЕФзјБъЮЊЃЈ4ЃЌ0ЃЉЪБЃЌ
ЂйдкЕуDЃЈ3ЃЌ0ЃЉЃЌEЃЈ4ЃЌ1ЃЉЃЌFЃЈ7ЃЌ0ЃЉжаЃЌЕуAЙигкЁбCЕФЛЦН№ЕуЪЧ ЃЛ
ЂкжБЯп![]() ЩЯДцдкЕуAЙигкЁбCЕФЛЦН№ЕуPЃЌЧѓЕуPЕФКсзјБъЕФШЁжЕЗЖЮЇЃЛ
ЩЯДцдкЕуAЙигкЁбCЕФЛЦН№ЕуPЃЌЧѓЕуPЕФКсзјБъЕФШЁжЕЗЖЮЇЃЛ
(2)ШєyжсЩЯДцдкЕуAЙигкЁбCЕФЛЦН№ЕуЃЌжБНгаДГіЕуCКсзјБъЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
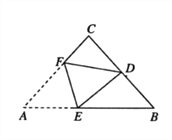
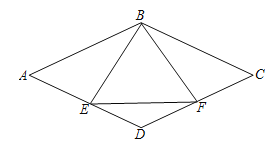
ЁОЬтФПЁПШчЭМЃЌЕуEЁЂFЗжБ№ЮЊСтаЮABCDБпADЁЂCDЕФжаЕу.
ЃЈ1ЃЉЧѓжЄЃКBE=BFЃЛ
ЃЈ2ЃЉЕБЁїBEFЮЊЕШБпШ§НЧаЮЪБЃЌЧѓжЄЃКЁЯD=2ЁЯA.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЬнаЮABCDжаЃЌADЁЮBCЃЌAB=CD=AD=5cm,BC=11cm,ЕуPДгЕуDПЊЪМбиDAБпвдУПУы1cmЕФЫйЖШвЦЖЏЃЌЕуQДгЕуBПЊЪМбиBCБпвдУПУы2cmЕФЫйЖШвЦЖЏЃЈЕБЕуPЕНДяЕуAЪБЃЌЕуPгыЕуQЭЌЪБЭЃжЙвЦЖЏЃЉЃЌМйЩшЕуPвЦЖЏЕФЪБМфЮЊxЃЈУыЃЉЃЌЫФБпаЮABQPЕФУцЛ§ЮЊyЃЈcm2ЃЉ.
(1)ЧѓyЙигкxКЏЪ§НтЮіЪНЃЌВЂаДГіЫќЕФЖЈвхгђЃЛ
(2)дквЦЖЏЕФЙ§ГЬжаЃЌPQЪЧЗёПЩФмЦНЗжЖдНЧЯпACЃПШєФмЃЌЧѓГіxЕФжЕЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЛ
(3)дквЦЖЏЕФЙ§ГЬжаЃЌЪЧЗёДгдкxЪЙЕУPQ=ABЃЌШєДцдкЧѓГіЫљгаxЕФжЕЃЌШєВЛДцдкЧыЫЕУїРэгЩ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЈвх[aЃЌbЃЌc]ЮЊКЏЪ§y=ax2+bx+cЕФЬиеїЪ§ЃЌЯТУцИјГіЬиеїЪ§ЮЊ[2mЃЌ1ЉmЃЌЉ1Љm]ЕФКЏЪ§ЕФвЛаЉНсТлЃЌЦфжаВЛе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
A. ЕБm=Љ3ЪБЃЌКЏЪ§ЭМЯѓЕФЖЅЕузјБъЪЧЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
B. ЕБmЃО0ЪБЃЌКЏЪ§ЭМЯѓНиxжсЫљЕУЕФЯпЖЮГЄЖШДѓгк![]()
C. ЕБmЁй0ЪБЃЌКЏЪ§ЭМЯѓОЙ§ЭЌвЛИіЕу
D. ЕБmЃМ0ЪБЃЌКЏЪ§дкx>![]() ЪБЃЌyЫцxЕФдіДѓЖјМѕаЁ
ЪБЃЌyЫцxЕФдіДѓЖјМѕаЁ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЫљЪОЃЌЃЈ1ЃЉвбжЊDЪЧЕШбќЁїABCЕзБпBCЩЯвЛЕуЃЌDEЁЮACЃЌНЛABгкЕуEЃЎDFЁЮABЃЌНЛACгкЕуFЃЎЧыФуЬНОПDEЁЂDFЁЂABжЎМфЕФЙиЯЕЃЌВЂЫЕУїРэгЩЃЎЃЈ2ЃЉШчЭМ2ЫљЪОЃЌвбжЊDЪЧЕШбќЁїABCЕзБпBCбгГЄЯпЩЯвЛЕуЃЌDEЁЮACЃЌНЛBAЕФбгГЄЯпгкЕуEЃЎDFЁЮABЃЌНЛACЕФбгГЄЯпгкЕуFЃЎЧыФуЬНОПDEЁЂDFЁЂABжЎМфЕФЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
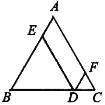
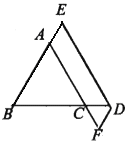
ЭМ1 ЭМ2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
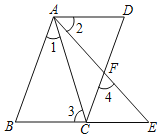
ЁОЬтФПЁПШчЭМЃЌвбжЊЫФБпаЮABCDЃЌABЁЮCDЃЌЕуEЪЧBCбгГЄЯпЩЯвЛЕуЃЌСЌНгACЁЂAEЃЌAEНЛCDгкЕуFЃЌЁЯ1=ЁЯ2ЃЌЁЯ3=ЁЯ4ЃЎ
жЄУїЃК
ЃЈ1ЃЉЁЯBAE=ЁЯDACЃЛ
ЃЈ2ЃЉЁЯ3=ЁЯBAEЃЛ
ЃЈ3ЃЉADЁЮBEЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com