
【题目】每天你是如何醒来的?某校有4000名学生,从不同班级不同层次抽取了400名学生进行调查,下表是这400名学生早晨起床方式的统计表:
起床方式 | 人数/人 |
别人叫醒 | 172 |
闹钟 | 88 |
自己醒来 | 64 |
其他 | 76 |
回答下列问题:
(1)该问题中总体是________;
(2)样本是__________;样本容量是__________.
(3)个体是________;
(4)估计全校学生中自己醒来的人数为________人.
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
(1)当∠BDA=115°时,∠EDC= °,∠DEC= °;点D从B向C运动时,∠BDA逐渐变 (填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数.若不可以,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上,另一个顶
点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图(3),
则三角板的最大边的长为( )
A. ![]() B.
B. ![]() C.
C.![]()
![]() D.
D. ![]()
![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA⊥OB,AB⊥x轴于C,点A(![]() ,1)在反比例函数y=
,1)在反比例函数y=![]() 的图象上.
的图象上.
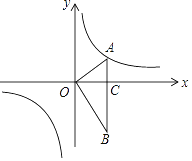
(1)求反比例函数y=![]() 的表达式;
的表达式;
(2)在x轴上存在一点P,使S△AOP= ![]() S△AOB, 求点P的坐标.
S△AOB, 求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图,若双曲线![]() (k>0)与它的其中一条对称轴y=x相交于两点A,B,则线段AB的长称为双曲线
(k>0)与它的其中一条对称轴y=x相交于两点A,B,则线段AB的长称为双曲线![]() (k>0)的对径.
(k>0)的对径.
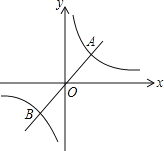
(1)求双曲线![]() 的对径;
的对径;
(2)若某双曲线![]() (k>0)的对径是
(k>0)的对径是![]() .求k的值.
.求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
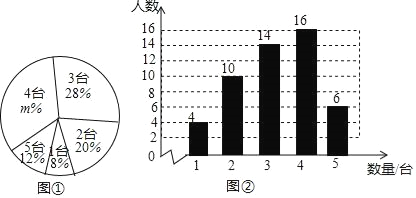
【题目】随着移动计算技术和无线网络的快速发展,移动学习方式越来越引起人们的关注,某校计划将这种学习方式应用到教育学中,从全校1500名学生中随机抽取了部分学生,对其家庭中拥有的移动设备的情况进行调查,并绘制出如下的统计图①和图②,根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为 ,图①中m的值为 ;
(2)求本次调查获取的样本数据的众数、中位数和平均数;
(3)根据样本数据,估计该校1500名学生家庭中拥有3台移动设备的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,∠ABC=2∠C,以B为圆心任意长为半径作弧,交BA、BC于点E. F,分别以E. F为圆心,以大于![]() EF的长为半径作弧,两弧交于点P,作射线BP交AC于点,则下列说法不正确的是( )
EF的长为半径作弧,两弧交于点P,作射线BP交AC于点,则下列说法不正确的是( )

A.∠ADB=∠ABCB.AB=BDC.AC=AD+BDD.∠ABD=∠BCD
查看答案和解析>>
科目:初中数学 来源: 题型:
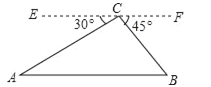
【题目】如图,从热气球C处测得地面A,B两点的俯角分别为30°,45°,此时热气球C处所在位置到地面上点A的距离为400米.求地面上A,B两点间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰Rt△ABC中,AB=AC,∠BAC=90°
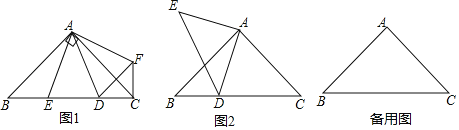
(1)如图1,D,E是等腰Rt△ABC斜边BC上两动点,且∠DAE=45°,将△ABE绕点A逆时针旋转90后,得到△AFC,连接DF
①求证:△AED≌△AFD;
②当BE=3,CE=7时,求DE的长;
(2)如图2,点D是等腰Rt△ABC斜边BC所在直线上的一动点,连接AD,以点A为直角顶点作等腰Rt△ADE,当BD=3,BC=9时,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com