
【题目】定义:如图,若双曲线![]() (k>0)与它的其中一条对称轴y=x相交于两点A,B,则线段AB的长称为双曲线
(k>0)与它的其中一条对称轴y=x相交于两点A,B,则线段AB的长称为双曲线![]() (k>0)的对径.
(k>0)的对径.
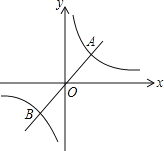
(1)求双曲线![]() 的对径;
的对径;
(2)若某双曲线![]() (k>0)的对径是
(k>0)的对径是![]() .求k的值.
.求k的值.
【答案】(1) 双曲线![]() 的对径是2
的对径是2![]() ;(2)25
;(2)25
【解析】
过A点作AC⊥x轴于C.
(1)先解方程组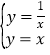 ,可得到A点坐标为(1,1),B点坐标为(-1,-1),即OC=AC=1,则△OAC为等腰直角三角形,得到OA=
,可得到A点坐标为(1,1),B点坐标为(-1,-1),即OC=AC=1,则△OAC为等腰直角三角形,得到OA=![]() OC=
OC=![]() ,则AB=2OA=2
,则AB=2OA=2![]() ,于是得到双曲线y=
,于是得到双曲线y=![]() 的对径;
的对径;
(2)根据双曲线的对径的定义得到当双曲线的对径为10![]() 即AB=10
即AB=10![]() ,OA=5
,OA=5![]() ,根据OA=
,根据OA=![]() OC=
OC=![]() AC,则OC=AC=5,得到点A坐标为(5,5),把A(5,5)代入双曲线y=
AC,则OC=AC=5,得到点A坐标为(5,5),把A(5,5)代入双曲线y=![]() (k>0)即可得到k的值.
(k>0)即可得到k的值.
过A点作AC⊥x轴于C,如图:
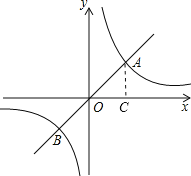
(1)解方程组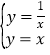 ,得
,得![]() ,
,![]() ,
,
∴A点坐标为(1,1),B点坐标为(﹣1,﹣1),
∴OC=AC=1,
∴OA=![]() OC=
OC=![]() ,
,
∴AB=2OA=2![]() ,
,
∴双曲线![]() 的对径是2
的对径是2![]() ;
;
(2)∵双曲线的对径为10![]() 即AB=10
即AB=10![]() ,OA=5
,OA=5![]() ,
,
∴OA=![]() OC=
OC=![]() AC,
AC,
∴OC=AC=5,
∴点A坐标为(5,5),
把A(5,5)代入双曲线![]() (k>0)得k=5×5=25,
(k>0)得k=5×5=25,
即k的值为25.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
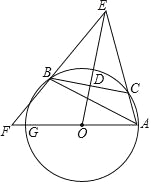
【题目】如图,已知△ABC内接于⊙O,点C在劣弧AB上(不与点A,B重合),点D为弦BC的中点,DE⊥BC,DE与AC的延长线交于点E,射线AO与射线EB交于点F,与⊙O交于点G,设∠GAB=ɑ,∠ACB=β,∠EAG+∠EBA=γ,
(1)点点同学通过画图和测量得到以下近似数据:
ɑ | 30° | 40° | 50° | 60° |
β | 120° | 130° | 140° | 150° |
γ | 150° | 140° | 130° | 120° |
猜想:β关于ɑ的函数表达式,γ关于ɑ的函数表达式,并给出证明:
(2)若γ=135°,CD=3,△ABE的面积为△ABC的面积的4倍,求⊙O半径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠B=90°![]() ∠A
∠A
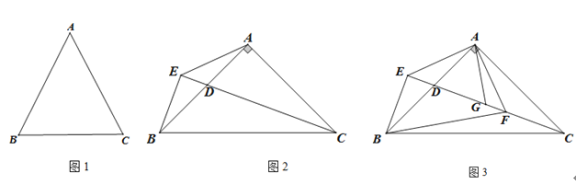
(1)如图1,求证:AB=AC;
(2)如图2,若∠BAC=90°,点D为AB上一点,过点B作直线CD的垂线,垂足为E,连接AE, 求∠AEC的度数;
(3)如图3,在(2)的条件下,过点A作AE的垂线交CE于点F,连接BF,若∠ABF-∠EAB=15°,G为DF上一点,连接AG,若∠AGD=∠EBF,AG=6,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每天你是如何醒来的?某校有4000名学生,从不同班级不同层次抽取了400名学生进行调查,下表是这400名学生早晨起床方式的统计表:
起床方式 | 人数/人 |
别人叫醒 | 172 |
闹钟 | 88 |
自己醒来 | 64 |
其他 | 76 |
回答下列问题:
(1)该问题中总体是________;
(2)样本是__________;样本容量是__________.
(3)个体是________;
(4)估计全校学生中自己醒来的人数为________人.
查看答案和解析>>
科目:初中数学 来源: 题型:
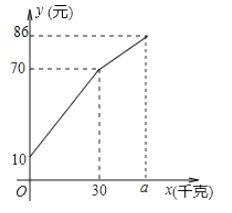
【题目】一农民带了土豆进城出售,为了方便,他带了一些零用钱备用,按市场价出售一些土豆后,又降价出售,售出土豆的千克数![]() 与他手中持有的钱数
与他手中持有的钱数![]() (含零用钱)的关系如图.结合图象回答:
(含零用钱)的关系如图.结合图象回答:
(1)农民自带的零钱是多少元?
(2)求出降价前![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)降价后他按每千克1.6元将土豆售完,这时他手中的钱(含零用钱)是86元,那么他一共带了多少土豆去城里出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在直角![]() 中,
中,![]() ,点
,点![]() 是
是![]() 中点,连接
中点,连接![]() ,点
,点![]() 为
为![]() 的中点,过点
的中点,过点![]() 作
作![]() 交线段
交线段![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .
.
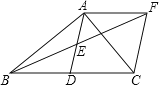
(1)求证:![]() ;
;
(2)在不添加任何辅助线的情况下,请直接写出所有面积等于![]() 面积
面积![]() 倍的三角形.
倍的三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高尔夫运动员将一个小球沿与地面成一定角度的方向击出,在不考虑空气阻力的条件下,小球的飞行高度h(m)与它的飞行时间(s)满足二次函数关系,t与h的几组对应值如下表所示:
t(s) | 0 | 0.5 | 1 | 1.5 | 2 | … |
h(m) | 0 | 8.75 | 15 | 18.75 | 20 | … |
(1)求h与t之间的函数关系式(不要求写t的取值范围);
(2)求小球飞行3s时的高度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com