
����Ŀ�������������������ڹ��������̼ۣ���������ʱ�ļ۸�ÿ��24Ԫ�����ij��˾��Ʊ1000�ɣ����������չ��в����ף��ڽ�������һ�ܽ������ڣ���������¸ù�ÿ�����̼۸����ǰһ����ǵ�������±�������λ��Ԫ��

��1������������ʱ��ÿ���Ƕ���Ԫ��
��2����֪С�����������Ʊʱ����1.5��������ѣ�����ʱ�踶�ɽ����1.5��������Ѻ�1��Ľ���˰�����������������ǰ��ȫ����Ʊ�������������������Σ�
���𰸡���1������������ʱ���ù�Ʊÿ��27.5Ԫ����2�������������Ϊ��4891.5Ԫ��
��������
��1�������������ļӼ��������㷽�����������������ʱ���ù�Ʊÿ�ɶ���Ԫ���ɣ�
��2���ñ����������̼۽�ȫ����Ʊ������õ���Ǯ����ȥ�����Ʊ��������Ʊ����֧���Ľ��ѣ��жϳ��������������μ��ɣ�
��1��24+4-1.5+1=27.5��Ԫ��
������������ʱ���ù�Ʊÿ��27.5Ԫ��
��2��24+4-1.5+1+2-0.5=29��Ԫ��
29��1000-29��1000�� (1.5��+1��)-24��1000��(1+1.5��)=4891.5
�������������Ϊ��4891.5Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�
��![]() ����
����![]() �ڱ�
�ڱ�![]() �ϣ���
�ϣ���![]() ��
��![]() ��
��![]() ������
������![]() ���ӳ�
���ӳ�![]() ����
����![]() �ڵ�
�ڵ�![]() ����
����![]() ���н��ۣ���
���н��ۣ���![]() ��
��![]() ��
��![]() ��
��![]()
������ȷ���۵ĸ����� �� ��
A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
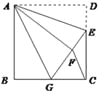
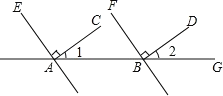
����Ŀ����ͼ,��֪AC��AE,BD��BF,��1=35��,��2=35����AC��BDƽ����?AE��BFƽ����?
��Ϊ��1=35��,��2=35��(��֪)�����ԡ�1=��2.����___��___( ).
����ΪAC��AE(��֪)�����ԡ�EAC=90��( )
���ԡ�EAB=��EAC+��1=125��.
ͬ���ɵ�,��FBG=��FBD+��2=__ ��.
���ԡ�EAB=��FBG( ).
����___��___(ͬλ�����,��ֱ��ƽ��).
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�ᳫ��Լ��ˮ����������ˮ��˾ÿ��ֻ��ij��λ�ƻ�����ˮ200�֣��ƻ�����ˮÿ���շ�2.4Ԫ�����ƻ�����ÿ�ְ�3.6Ԫ�շѣ�
���ô���ʽ��ʾ�������⣨������軯�� ��������ˮ��Ϊ![]() �֣�����ˮ��С�ڵ���200��ʱ���踶�����Ԫ������ˮ������200��ʱ���踶�����Ԫ��
�֣�����ˮ��С�ڵ���200��ʱ���踶�����Ԫ������ˮ������200��ʱ���踶�����Ԫ��
����ij��λ4�·ݽ���ˮ��840Ԫ����õ�λ��ˮ�����ٶ֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧ����������ijУ��1����ѧ����ĩ����ѧ�ɼ����ɼ�ȡ����������Ϊ100�֣�����ͳ�ƣ����������ÿ���˵ijɼ�������ͬ�����ݴ˻��Ƴ�����Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ���������ͼ���ṩ����Ϣ������������⣺
���� | 49.5��59.5 | 59.5��69.5 | 69.5��79.5 | 79.5��89.5 | 89.5��100.5 | �ϼ� |
Ƶ�� | 2 | 8 | 20 | a | 4 | c |
Ƶ�� | 0.04 | b | 0.40 | 0.32 | 0.08 | 1 |
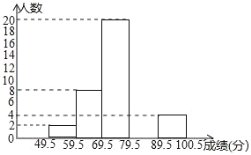
��1��Ƶ����Ƶ�ʷֲ�����a=____��b=_____��c=_____��
��2����ȫƵ���ֲ�ֱ��ͼ��
��3�����Ҫ���ð���ѧ����ĩ��ѧ�ɼ�������ͳ��ͼ����ô������69.5��79.5֮�������Բ�ĽǵĶ�����_______��
��4������ͬѧ�ɼ�Ϊ79�֣���˵�������ǰ��ϱ��ҳɼ��ߵ��˻���![]() ����Ҫ����Ŭ����������˵����ȷ����˵�����ɣ�
����Ҫ����Ŭ����������˵����ȷ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ABCD�ı߳���1����E��CD���ϵ��е�.PΪ������ABCD���ϵ�һ�����㣬����P��A���������![]() �˶��������E.����P������·��Ϊ�Ա���x��
�˶��������E.����P������·��Ϊ�Ա���x��![]() �����Ϊ�����y����
�����Ϊ�����y����![]() ʱ��x��ֵ����_________��
ʱ��x��ֵ����_________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
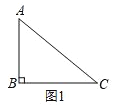
����Ŀ������̽����
(1)��ͼ1,�ڡ�ABC��,��B=90��AB=3��BC=4������ABC�ı��ϴ��ڵ�P��ʹ��ABP����ABΪ���ĵ��������Σ���CP�ij�Ϊ______��
(2)��ͼ2,�ھ���ABCD��,AB=3,��BC�ϴ��ڵ�P,ʹ��APD=90�������ABCD�������Сֵ.
��������
(3)��ͼ3,���ı���ABCD��,AB=3,��A=��B=90,��C=45,��CD�ϴ��ڵ�P,ʹ��APB=60�㣬�ڴ������£��ı���ABCD������Ƿ�������ֵ?�����ڣ�������ֵ���������ڣ���˵������.
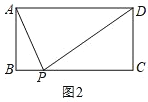
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ��ڢ�С��ļ��㷽�����ټ���ڢ�С�⣮
���C5![]() +���C9
+���C9![]() ��+17
��+17![]() +���C3
+���C3![]() ��
��
�⣺ԭʽ=[���C5��+���C![]() ��]+[���C9��+���C
��]+[���C9��+���C![]() ��]+��17+
��]+��17+![]() ��+[���C3+���C
��+[���C3+���C![]() ��]
��]
=[���C5��+���C9��+���C3��+17]+[���C![]() ��+���C
��+���C![]() ��+���C
��+���C![]() ��+
��+![]() ]
]
=0+���C1![]() ��
��
=�C1![]() ��
��
�������ַ������������������üӷ��Ľ����ɡ�����ɿ�ʹ�����㣮
�ڷ�������ķ������㣺����2000![]() ��+����1999
��+����1999![]() ��+4000
��+4000![]() +����1
+����1![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣�����ABC�У���ACB=90�㣬��B=30�㣬AC=1��DΪAB���е㣬EFΪ��ACD ����λ�ߣ��ı���EFGHΪ��ACD���ڽӾ��Σ����ε��ĸ����������ACD�ı��ϣ���
��1���������EFGH�������
��2��������EFGH��AB����ƽ�ƣ�F����BC��ʱֹͣ�ƶ�����ƽ�ƹ����У�����������CBD�ص����ֵ����Ϊ![]() ʱ�������ƽ�Ƶľ��룻
ʱ�������ƽ�Ƶľ��룻
��3����ͼ�ۣ�����2���о���ƽ��ֹͣʱ���õľ��μ�Ϊ����![]() ��������
��������![]() ��
��![]() �㰴˳ʱ�뷽����ת����
�㰴˳ʱ�뷽����ת����![]() ����CD��ʱֹͣת������ת��ľ��μ�Ϊ����
����CD��ʱֹͣת������ת��ľ��μ�Ϊ����![]() ������ת��Ϊ
������ת��Ϊ![]() ����
����![]() ��ֵ��
��ֵ��
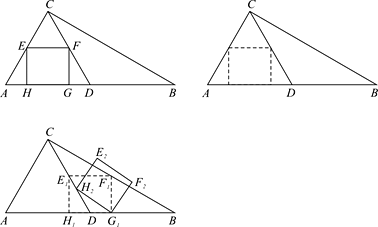
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com