
 如图,一天,我国一渔政船航行到A处时,发现正东方向的我领海区域B处有一可疑渔船,正在以20海里/小时的速度向西北方向航行,我渔政船立即沿北偏东60°方向航行,1.5小时后,在我领海区域的C处截获可疑渔船,我渔政船的航行路程是30$\sqrt{2}$海里.
如图,一天,我国一渔政船航行到A处时,发现正东方向的我领海区域B处有一可疑渔船,正在以20海里/小时的速度向西北方向航行,我渔政船立即沿北偏东60°方向航行,1.5小时后,在我领海区域的C处截获可疑渔船,我渔政船的航行路程是30$\sqrt{2}$海里. 分析 作CD⊥AB于点D,垂足为D,首先在Rt△BCD中求得CD的长,然后在Rt△ACD中求得AC的长即可.
解答 解:作CD⊥AB于点D,垂足为D,
在Rt△BCD中,
∵BC=20×1.5=30(海里),∠CBD=45°,
∴CD=BC•sin45°=30×$\frac{\sqrt{2}}{2}$=15$\sqrt{2}$(海里),
则在Rt△ACD中,
AC=$\frac{CD}{sim30°}$=15$\sqrt{2}$×2=30$\sqrt{2}$(海里).
故答案为30$\sqrt{2}$.
点评 本题考查了解直角三角形的应用,解题的关键是从实际问题中构造出直角三角形并利用三角函数的知识求解.


科目:初中数学 来源: 题型:解答题
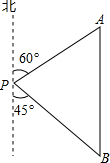 五一期间,小明到美丽的黄山参加社会实践活动,在景点P处测得景点B位于南偏东45°方向;然后沿北偏东60°方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与B之间的距离.(参考数据:$\sqrt{3}$≈1.732,结果精确到0.1米)
五一期间,小明到美丽的黄山参加社会实践活动,在景点P处测得景点B位于南偏东45°方向;然后沿北偏东60°方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与B之间的距离.(参考数据:$\sqrt{3}$≈1.732,结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
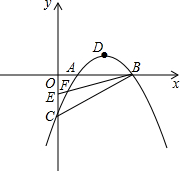 已知抛物线y=ax2+bx+c与x轴交于A(1,0),B(3,0),与y轴交于C(0,-2),顶点为D,点E的坐标为(0,-1),该抛物线于BE交于另一点F,连接BC
已知抛物线y=ax2+bx+c与x轴交于A(1,0),B(3,0),与y轴交于C(0,-2),顶点为D,点E的坐标为(0,-1),该抛物线于BE交于另一点F,连接BC查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校七年级有400名学生,在一次生物测验后,为了解本次测验的成绩情况,从中随机取了部分学生的成绩进行统计,并绘制了如下图表:
某校七年级有400名学生,在一次生物测验后,为了解本次测验的成绩情况,从中随机取了部分学生的成绩进行统计,并绘制了如下图表:| 等级 | 分数 | 频数 | 频率 |
| A | 90≤x≤100 | 6 | 0.15 |
| B | 80≤x<90 | 20 | a |
| C | 70≤x<80 | b | 0.2 |
| D | 60≤x<70 | c | 0.15 |
| 合计 | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com