
【题目】请阅读以下材料,并完成相应的任务:

任务:
(1)设P(a,![]() ),R(b,
),R(b,![]() ),求直线OM的函数解析式(用含a,b的代数式表示),并说明Q点在直线OM上;
),求直线OM的函数解析式(用含a,b的代数式表示),并说明Q点在直线OM上;
(2)证明:∠MOB=![]() ∠AOB.
∠AOB.
【答案】(1)![]() ,说明见解析;(2)见解析
,说明见解析;(2)见解析
【解析】
(1)根据题意,得M(b,![]() ),再进一步运用待定系数法求解;根据题意,得Q(a,
),再进一步运用待定系数法求解;根据题意,得Q(a,![]() ),代入求得的直线解析式说明Q点在直线OM上;
),代入求得的直线解析式说明Q点在直线OM上;
(2)连接PR,交OM于点S,结合矩形的性质、等腰三角形的性质和三角形的外角的性质即可证明;
(1)解:设直线OM的函数表达式为y=kx,
由题意可得四边形PQRM为矩形,且P(a,![]() ),R(b,
),R(b,![]() ),
),
∴M(b,![]() ),Q(a,
),Q(a,![]() )
)
把点M(b,![]() )代入y=kx得k=
)代入y=kx得k=![]()
∴直线OM的函数表达式为![]()
∵Q的坐标(a,![]() )满足
)满足![]() ,
,
∴点Q在直线OM上.
(2)证明:连接PR,交OM于点S
由题意得四边形PQRM是矩形,
∴PR=QM
而SP=![]() PR,SM=
PR,SM=![]() QM,
QM,
∴SP= SM
∴∠1=∠2.
∴∠3=∠1+∠2=2∠2
∵PR=2PO,
∴PS=PO.
∴∠4=∠3=2∠2.
∵PM∥x轴
∴∠2=∠5.
∴∠AOB=∠4+∠5=3∠5.
即∠MOB=![]() ∠AOB
∠AOB



科目:初中数学 来源: 题型:
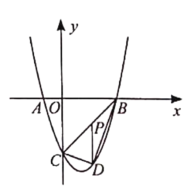
【题目】在平面直角坐标系中,抛物线![]() 经过点A、B、C,已知A(-1,0),B(3,0),C(0,-3).
经过点A、B、C,已知A(-1,0),B(3,0),C(0,-3).
(1)求此抛物线的函数表达式;
(2)若P为线段BC上一点,过点P作![]() 轴的平行线,交抛物线于点D,当△BCD面积最大时,求点P的坐标;
轴的平行线,交抛物线于点D,当△BCD面积最大时,求点P的坐标;
(3)若M(m,0)是![]() 轴上一个动点,请求出CM+
轴上一个动点,请求出CM+![]() MB的最小值以及此时点M的坐标.
MB的最小值以及此时点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y=![]() 的图象经过点A(4,m),AB⊥x轴,且△AOB的面积为2.
的图象经过点A(4,m),AB⊥x轴,且△AOB的面积为2.
(1)求k和m的值;
(2)若点C(x,y)也在反比例函数y=![]() 的图象上,当-3≤x≤-1时,求函数值y的取值范围.
的图象上,当-3≤x≤-1时,求函数值y的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
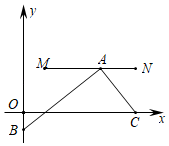
【题目】如图,在平面直角坐标系中,M、N、C三点的坐标分别为(![]() ,1),(3,1),(3,0),点A为线段MN上的一个动点,连接AC,过点A作AB⊥AC交y轴于点B,当点A从M运动到N时,点B随之运动,设点B的坐标为(0,b),则b的取值范围是( )
,1),(3,1),(3,0),点A为线段MN上的一个动点,连接AC,过点A作AB⊥AC交y轴于点B,当点A从M运动到N时,点B随之运动,设点B的坐标为(0,b),则b的取值范围是( )
A.![]() ≤b≤1B.
≤b≤1B.![]() ≤b≤1C.
≤b≤1C.![]() ≤b≤
≤b≤![]() D.
D.![]() ≤b≤1
≤b≤1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在中国数学名著《九章算术》中,有这样一个问题:“今有共买牛,七家共出一百九十,不足三百三十;九家共出二百七十,盈三十. 问家数、牛价各几何?”大意是:几家人凑钱合伙买牛,如果每7家共出190元,那么还缺少330元钱;如果每9家共出270元,又多了30元钱. 问共有多少人家,每头牛的价钱是多少元?若设有x户人家,则可列方程为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
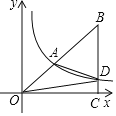
【题目】如图,反比例函数y=![]() (x>0)的图象经过Rt△BOC斜边上的中点A,与边BC交于点D,连接AD,则△ADB的面积为( )
(x>0)的图象经过Rt△BOC斜边上的中点A,与边BC交于点D,连接AD,则△ADB的面积为( )
A.12B.16C.20D.24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“一带一路”为我们打开了交流、合作的大门,也为沿线各国在商贸等领域提供了更多的便捷,2018年11月5日至10日,首届中国国际进口博览会在国家会展中心(上海)举办,据哈外贸商会发布消息,博览会期间,哈Paseka公司与重庆某国际贸易公司签订了供应蜂蜜合同:哈Paseka公司于2019年6月前分期分批向重庆某国际贸易公司供给优质蜂蜜共3000万件,该公司顺应新时代购物流,打算分线上和线下两种方式销售.
(1)若计划线上销售量不低于线下销售量的25%,求该公司计划在线下销售量最多为多少万件?
(2)该公司在12月上旬销售优质蜂蜜共240万件,且线上线下销售单件均为100元/件.12月中旬决定线上销售单价下调m%,线下销售单价不变,在这种情况下,12月中旬销售总量比上旬增加了m%,且中旬线上销售量占中旬总销量的![]() ,结果中旬销售总金额比上旬销售总金额提高了
,结果中旬销售总金额比上旬销售总金额提高了![]() m%.求m的值.
m%.求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC是⊙O的弦,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E,连接BD.
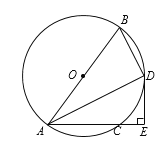
(1)求证:DE是⊙O的切线;
(2)若BD=3,AD=4,则DE= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (a≠0)交x轴于A、B两点,A点坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC交抛物线于点G.
(a≠0)交x轴于A、B两点,A点坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC交抛物线于点G.
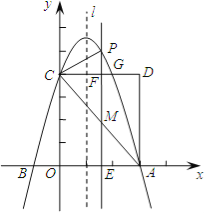
(1)求抛物线的解析式;
(2)抛物线的对称轴l在边OA(不包括O、A两点)上平行移动,分别交x轴于点E,交CD于点F,交AC于点M,交抛物线于点P,若点M的横坐标为m,请用含m的代数式表示PM的长;
(3)在(2)的条件下,连结PC,则在CD上方的抛物线部分是否存在这样的点P,使得以P、C、F为顶点的三角形和△AEM相似?若存在,求出此时m的值,并直接判断△PCM的形状;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com