
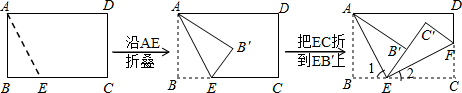
分析 (1)由邻补角的性质直接得出.
(2)根据折叠的性质可知,∠1=∠AEB,∠2=∠FEC,而这四个角的和为180°,从而求得∠1+∠2的度数.
解答 解;(1)∠1与∠AEC互补,;∠2与∠FEB互补;
(2)∠1+∠2=90°.理由:
根据折叠的性质可知,∠1=∠AEB,∠2=∠FEC,
∵∠1+∠AEB+∠2+∠FEC=180°,
∴2(∠1+∠2)=180°,即∠1+∠2=90°;
(3)AE与EF垂直
∵由(2)知∵∠1+∠AEB+∠2+∠FEC=180°∠1+∠2=90°,
∴∠AEB+∠FEC=90°,
∴AE与EF垂直.
点评 本题考查了余角,补角的定义,垂线的性质,图形的翻折变换等知识点,准确识别图形是解题的关键.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
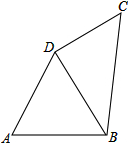 如图,在四边形ABCD中,AB=AD=8,∠A=60°,∠ADC=150°,四边形ABCD的周长为32.
如图,在四边形ABCD中,AB=AD=8,∠A=60°,∠ADC=150°,四边形ABCD的周长为32.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
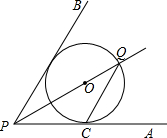 如图,点O在∠APB的平分线上,⊙O与PA相切于点C.
如图,点O在∠APB的平分线上,⊙O与PA相切于点C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com