
【题目】如图,已知二次函数y=ax2+bx+4的图象与x轴交于点A(4,0)和点D(﹣1,0),与y轴交于点C,过点C作BC平行于x轴交抛物线于点B,连接AC
(1)求这个二次函数的表达式;
(2)点M从点O出发以每秒2个单位长度的速度向点A运动;点N从点B同时出发,以每秒1个单位长度的速度向点C运动,其中一个动点到达终点时,另一个动点也随之停动,过点N作NQ垂直于BC交AC于点Q,连结MQ.
①求△AQM的面积S与运动时间t之间的函数关系式,写出自变量的取值范围;当t为何值时,S有最大值,并求出S的最大值;
②是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标;若不存在,说明理由.
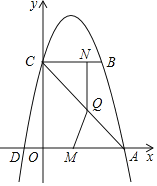
【答案】(1)y=﹣x2+3x+4;(2)①S=-t2+t+2;0≤t≤2;t=![]() 时,S最大值=
时,S最大值=![]() ;②存在,点M的坐标分别为(1,0)和(2,0).
;②存在,点M的坐标分别为(1,0)和(2,0).
【解析】
(1)由待定系数法将AD两点代入即可求解.
(2)①分别用t表示出AM、PQ,由三角形面积公式直接写出含有t的二次函数关系式,由二次函数的最大值可得答案;
②分类讨论直角三角形的直角顶点,然后解出t,求得M坐标.
(1)∵二次函数的图象经过A(4,0)和点D(﹣1,0),
∴![]() ,
,
解得![]() ,
,
所以,二次函数的解析式为y=﹣x2+3x+4.
(2)①延长NQ交x轴于点P,
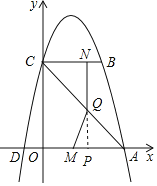
∵BC平行于x轴,C(0,4)
∴B(3,4),NP⊥OA.
根据题意,经过t秒时,NB=t,OM=2t,
则CN=3﹣t,AM=4﹣2t.
∵∠BCA=∠MAQ=45°,
∴QN=CN=3﹣t,
∴PQ=NP﹣NQ=4﹣(1﹣t)=1+t,
∴S△AMQ=![]() AM×PQ=
AM×PQ=![]() (4-2t)(1+t)
(4-2t)(1+t)
=﹣t2+t+2.
∴S=-t2+t+2=-(t-![]() )2+
)2+![]() .
.
∵a=﹣1<0,且0≤t≤2,∴S有最大值.
当t=![]() 时,S最大值=
时,S最大值=![]() .
.
②存在点M,使得△AQM为直角三角形.
设经过t秒时,NB=t,OM=2t,
则CN=3﹣t,AM=4﹣2t,
∴∵∠BCA=∠MAQ=45°.
Ⅰ.若∠AQM=90°,
则PQ是等腰Rt△MQA底边MA上的高.
∴PQ是底边MA的中线,
∴PQ=AP=![]() MA,
MA,
∴1+t=![]() (4﹣2t),
(4﹣2t),
解得,t=![]() ,
,
∴M的坐标为(1,0).
Ⅱ.若∠QMA=90°,此时QM与QP重合.
∴QM=QP=MA,
∴1+t=4﹣2t,
∴t=1,
∴点M的坐标为(2,0).
所以,使得△AQM为直角三角形的点M的坐标分别为(1,0)和(2,0).


科目:初中数学 来源: 题型:
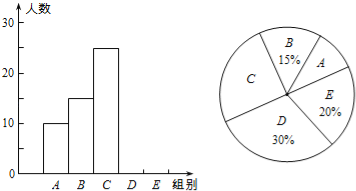
【题目】某校举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.
组别 | 正确字数x | 人数 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | n |
根据以上信息解决下列问题:
(1)在统计表中,m= ,n= ,并补全条形统计图.
(2)扇形统计图中“C组”所对应的圆心角的度数是 .
(3)若该校共有900名学生,如果听写正确的个数少于24个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
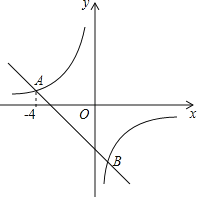
【题目】在平面直角坐标系xOy中,一次函数y=-x+k的图象与反比例函数y=-![]() 的图象交于点A(-4,n)和点B.
的图象交于点A(-4,n)和点B.
(1)求k的值和点B的坐标;
(2)若P是x轴上一点,且AP=AB,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
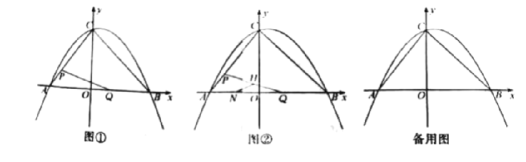
【题目】如图①,在平面直角坐标系中,ニ次函数![]() 的图像与坐标轴交于A,B,C三点,其中点A的坐标为(-3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点0出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ
的图像与坐标轴交于A,B,C三点,其中点A的坐标为(-3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点0出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ
(1)填空:b=_, c=_;
(2)在点P,Q运动过程中,△APQ可能是直角三角形吗?请说明理由;
(3)如图2,点N的坐标为![]() ,线段PQ的中点为H,连接NH,当点Q关于直线NH的对称点Q`恰好落在线段BC上时,请直接写出点Q`的坐标
,线段PQ的中点为H,连接NH,当点Q关于直线NH的对称点Q`恰好落在线段BC上时,请直接写出点Q`的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
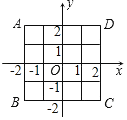
【题目】如图,在直角坐标系中的正方形ABCD边长为4,正方形ABCD的中心为原点O.现做如下实验:抛掷一枚均匀的正方体的骰子(六个面分别标有1至6这六个点数中的一个),每个面朝上的机会是相同的,连续抛掷两次,将骰子朝上的点数作为直角坐标系中点P的坐标(第次的点数作为横坐标,第二次的点数作为纵坐标)
(1)求点P落在正方形ABCD面上(含正方形内部和边界)的概率;
(2)试将正方形ABCD平移整数个单位,则是否存在一种平移,使点P落在正方形ABCD面上的概率为![]() ?若存在,请指出平移方式;若不存在,请说明理由.
?若存在,请指出平移方式;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2米,两拉索底端距离AD为20米,请求出立柱BH的长.(结果精确到0.1米, ![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】江门旅游文化节开幕前,某茶叶公司预测今年茶叶能够畅销,就用32000元购进了一批茶叶,上市后很快脱销,茶叶公司又用68000元购进第二批茶叶,所购数量是第一批购进数量的2倍,但每千克茶叶进价多了10元.
(1)该茶叶公司两次共购进这种茶叶多少千克?
(2)如果这两批茶叶每千克的售价相同,且全部售完后总利润率不低于20%,那么每千克售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一科技小组进行了机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上,甲、乙两机器人分别从A、B两点同时同向出发,历时7min同时到达C点,甲机器人前3分钟以a m/min的速度行走,乙机器人始终以60m/min的速度行走,如图是甲、乙两机器人之间的距离y(m)与他们的行走时间x(min)之间的函数图象,请结合图象,回答下列问题:
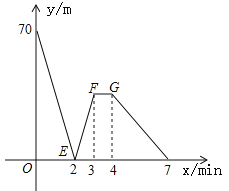
(1)A、B两点之间的距离是____m,A、C两点之间的距离是____m,a=____m/min;
(2)求线段EF所在直线的函数解析式;
(3)设线段FG∥x轴.
①当3≤x≤4时,甲机器人的速度为____m/min;
②直接写出两机器人出发多长时间相距28m.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com