
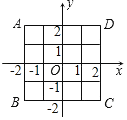
����Ŀ����ͼ����ֱ������ϵ�е�������ABCD�߳�Ϊ4��������ABCD������Ϊԭ��O����������ʵ�飺����һö���ȵ������������(������ֱ����1��6�����������е�һ��)��ÿ���泯�ϵĻ�������ͬ�ģ������������Σ������ӳ��ϵĵ�����Ϊֱ������ϵ�е�P������(�ڴεĵ�����Ϊ�����꣬�ڶ��εĵ�����Ϊ������)
(1)���P����������ABCD����(���������ڲ��ͱ߽�)�ĸ��ʣ�
(2)�Խ�������ABCDƽ����������λ�����Ƿ����һ��ƽ�ƣ�ʹ��P����������ABCD���ϵĸ���Ϊ![]() �������ڣ���ָ��ƽ�Ʒ�ʽ���������ڣ���˵�����ɣ�
�������ڣ���ָ��ƽ�Ʒ�ʽ���������ڣ���˵�����ɣ�
���𰸡�![]() ��(2)��������ABCD��������2����λ����������1����λ����������ABCD��������1����λ����������2����λ��
��(2)��������ABCD��������2�������������1�������������ABCD��������1�������������2�����
��������
(1)�����������г�ͼ��ó����ɵ�P������������͵�P����������ABCD����(���������ڲ��ͱ߽�)���������Ȼ����ݸ��ʹ�ʽ���ɵó��𰸣�
(2)Ҫʹ��P����������ABCD���ϵĸ���Ϊ![]() ���͵����ϻ�������������λƽ�ƣ����ԣ���������Ҫ���ƽ�Ʒ�ʽ�����֣���������ABCD��������2����λ����������1����λ����������ABCD��������1����λ����������2����λ��
���͵����ϻ�������������λƽ�ƣ����ԣ���������Ҫ���ƽ�Ʒ�ʽ�����֣���������ABCD��������2����λ����������1����λ����������ABCD��������1����λ����������2����λ��
(1)�б����£�
P�������� P����� | 1 | 2 | 3 | 4 | 5 | 6 |
1 | (1��1) | (1��2) | (1��3) | (1��4) | (1��5) | (1��6) |
2 | (2��1) | (2��2) | (2��3) | (2��4) | (2��5) | (2��6) |
3 | (3��1) | (3��2) | (3��3) | (3��4) | (3��5) | (3��6) |
4 | (4��1) | (4��2) | (4��3) | (4��4) | (4��5) | (4��6) |
5 | (5��1) | (5��2) | (5��3) | (5��4) | (5��5) | (5��6) |
6 | (6��1) | (6��2) | (6��3) | (6��4) | (6��5) | (6��6) |
���Թ��ɵ�P�����깲��36����������е�P��(1��1)��(1��2)��(2��1)��(2��2)�������������������ABCD���ϣ�
���Ե�P����������ABCD���ϵĸ���Ϊ![]() ��
��![]() ��
��
(2)��ΪҪʹ��P����������ABCD���ϵĸ���Ϊ![]() ��
��![]() ��
��![]() ������ֻ�ܽ�������ABCD���ϻ�������������λƽ�ƣ���ʹ��P�������������ϵ���ĿΪ12��
������ֻ�ܽ�������ABCD���ϻ�������������λƽ�ƣ���ʹ��P�������������ϵ���ĿΪ12��
���ԣ���������Ҫ���ƽ�Ʒ�ʽ�����֣��ֱ��ǣ���������ABCD��������2����λ����������1����λ(���������������)����������ABCD��������1����λ����������2����λ(���������������)��


 �㽭��У��ʦ���ϵ�д�
�㽭��У��ʦ���ϵ�д� ȫ�ų��100��ϵ�д�
ȫ�ų��100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
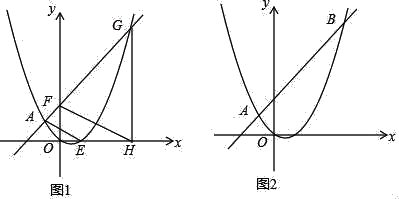
����Ŀ����֪��A����1��2����B��3��6����������y=ax2+bx��
(1)�������ߵĽ���ʽ��
(2)��ͼ1����F������Ϊ��0��m����m��2����ֱ��AF������������һ��G������G��x��Ĵ��ߣ�����ΪH������������x��������ύ�ڵ�E������FH��AE����֤��FH��AE��
(3)��ͼ2��ֱ��AB�ֱ�x�ᡢy����C��D���㣮��P�ӵ�C������������CD���������˶����ٶ�Ϊÿ��![]() ����λ���ȣ�ͬʱ��Q��ԭ��O��������x�������������˶����ٶ�Ϊÿ��1����λ���ȣ���M��ֱ��PQ�������ߵ�һ�����㣬���˶���t��ʱ��QM=2PM��ֱ��д��t��ֵ��
����λ���ȣ�ͬʱ��Q��ԭ��O��������x�������������˶����ٶ�Ϊÿ��1����λ���ȣ���M��ֱ��PQ�������ߵ�һ�����㣬���˶���t��ʱ��QM=2PM��ֱ��д��t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2013��12��2��1ʱ30�֣��й����������Ƿ������ijɹ������϶�������̽������������2013��12��15��4ʱ35�֣����϶�������̽�����������ú��������룬�����ú�������˳��ʻ��������棬�������й��������ϵĵ�һ���㼣�������ú�������һ���������Ϲ�����972�죬Լ23000Сʱ����23000�ÿ�ѧ��������ʾΪ��������
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ij�о��꼶ѧ��ѧҵ���������ɼ����ִ��������ȡ����ѧ���������ɼ�
���зֶΣ�A��50�֣�B��49-45�֣�C��44-40�֣�D��39-30�֣�E��29-0�֣�ͳ�����£�
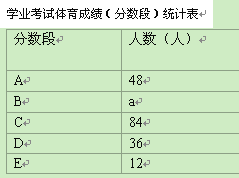
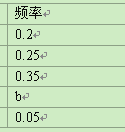
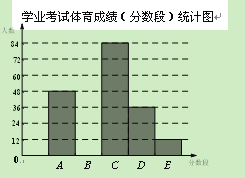
���������ṩ����Ϣ���ش��������⣺
��1����ͳ�Ʊ��У�a��ֵΪ �� ��b��ֵΪ �� ������ͳ��ͼ������������ܰ��ʾ����ͼʱ��������0.5���������ϵĺ�ɫǩ�ֱ�Ϳ������
��2����ͬѧ˵�����ҵ������ɼ��Ǵ˴γ��������������ݵ���λ��. �����ʣ���ͬѧ�������ɼ�Ӧ��ʲô�������ڣ� �� ������Ӧ�����ε���ĸ��
��3������ѳɼ���40�����ϣ���40�֣���Ϊ���㣬��ô���н���10440�����꼶ѧ���������ɼ�Ϊ�����ѧ������Լ�ж�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��PMN�У���P��90����PM��PN��MN��6cm���ھ���ABCD�У�AB��2cm��BC��6cm����C�͵�M�غϣ���B��C(M)��N��ͬһֱ������Rt��PMN����������ABCD��MN����ֱ����ÿ��1cm���ٶ������ƶ�������C���N�غ�Ϊֹ�����ƶ�x�����ABCD���PMN�ص����ֵ����Ϊycm2����y��x�Ĵ���ͼ����( )
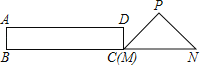
A. 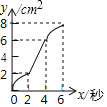 B.
B. 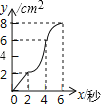
C. 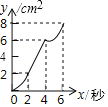 D.
D. 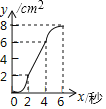
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ���y��ax2+bx+4��ͼ����x�ύ�ڵ�A(4��0)�͵�D(��1��0)����y�ύ�ڵ�C������C��BCƽ����x�ύ�������ڵ�B������AC
(1)��������κ����ı���ʽ��
(2)��M�ӵ�O������ÿ��2����λ���ȵ��ٶ����A�˶�����N�ӵ�Bͬʱ��������ÿ��1����λ���ȵ��ٶ����C�˶�������һ�����㵽���յ�ʱ����һ������Ҳ��֮ͣ��������N��NQ��ֱ��BC��AC�ڵ�Q������MQ.
�����AQM�����S���˶�ʱ��t֮��ĺ�����ϵʽ��д���Ա�����ȡֵ��Χ����tΪ��ֵʱ��S�����ֵ�������S�����ֵ��
���Ƿ���ڵ�M��ʹ�á�AQMΪֱ�������Σ������ڣ������M�����ꣻ�������ڣ�˵�����ɣ�
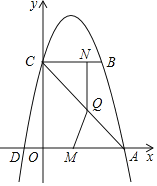
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
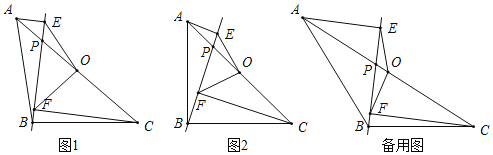
����Ŀ������ABC�У�AB=BC����O��AC���е㣬��P��AC�ϵ�һ�����㣨��P�����A��O��C�غϣ�������A����C��ֱ��BP�Ĵ��ߣ�����ֱ�Ϊ��E�͵�F������OE��OF��
��1����ͼ1����ֱ��д���߶�OE��OF��������ϵ��
��2����ͼ2������ABC=90��ʱ�����ж��߶�OE��OF֮���������ϵ��λ�ù�ϵ����˵������
��3����|CF��AE|=2��EF=2![]() ������POFΪ����������ʱ����ֱ��д���߶�OP�ij���
������POFΪ����������ʱ����ֱ��д���߶�OP�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
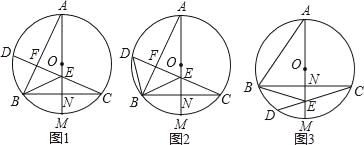
����Ŀ����֪AM�ǡ�Oֱ������BC��AM������Ϊ��N����CD��AM�ڵ�E������AB��BE��
��1����ͼ1����CD��AB������Ϊ��F����֤����BED��2��BAM��
��2����ͼ2���ڣ�1���������£�����BD������ABE����BDC����֤��AE��2CN��
��3����ͼ3��AB��CD��BE��CD��4��7��AE��11����EM�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
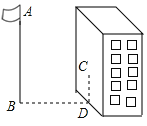
����Ŀ����ͼ����ijһʱ�̲��1�׳��������ֱ����ʱӰ��1.2�ף���ͬһʱ�����AB��Ӱ����ȫ����ˮƽ�����ϣ���һ��������¥����ǽ�ϣ�������ڵ����ϵ�Ӱ��BD=9.6�ף�����ǽ�ϵ�Ӱ��CD=2�ף�����˵ĸ߶�ABΪ____��.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com