
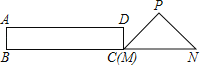
【题目】如图,在Rt△PMN中,∠P=90°,PM=PN,MN=6cm,在矩形ABCD中,AB=2cm,BC=6cm,点C和点M重合,点B,C(M),N在同一直线上若Rt△PMN不动,矩形ABCD沿MN所在直线以每秒1cm的速度向右移动,至点C与点N重合为止,设移动x秒后,矩形ABCD与△PMN重叠部分的面积为ycm2,则y与x的大致图象是( )
A. 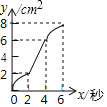 B.
B. 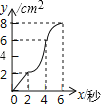
C. 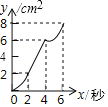 D.
D. 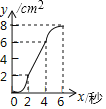
【答案】D
【解析】
在Rt△PMN中解题,要充分运用好垂直关系和45度角,因为此题也是点的移动问题,可知矩形ABCD以每秒1cm的速度由开始向右移动到停止,和Rt△PMN重叠部分的形状可分为下列三种情况,(1)0≤x≤2;(2)2<x≤4;(3)4<x≤6;根据重叠图形确定面积的求法,作出判断即可.
∵∠P=90°,PM=PN,
∴∠PMN=∠PNM=45°,
由题意得:CM=x,
分三种情况:
①当0≤x≤2时,如图1,边CD与PM交于点E,
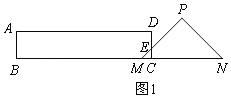
∵∠PMN=45°,
∴△MEC是等腰直角三角形,
此时矩形ABCD与△PMN重叠部分是△EMC,
∴y=S△EMC=![]() CMCE=
CMCE=![]() x2;
x2;
故选项A和B不正确;
②如图2,当D在边PN上时,过P作PF⊥MN于F,交AD于G,
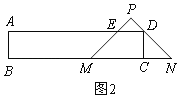
∵∠N=45°,CD=2,
∴CN=CD=2,
∴CM=6﹣2=4,
即此时x=4,
当2<x≤4时,如图3,矩形ABCD与△PMN重叠部分是四边形EMCD,
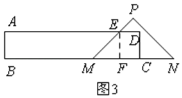
过E作EF⊥MN于F,
∴EF=MF=2,
∴ED=CF=x﹣2,
∴y=S梯形EMCD=![]() CD(DE+CM)=
CD(DE+CM)=![]() ×2×(x﹣2+x)=2x﹣2;
×2×(x﹣2+x)=2x﹣2;
③当4<x≤6时,如图4,矩形ABCD与△PMN重叠部分是五边形EMCGF,过E作EH⊥MN于H,
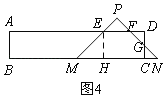
∴EH=MH=2,DE=CH=x﹣2,
∵MN=6,CM=x,
∴CG=CN=6﹣x,
∴DF=DG=2﹣(6﹣x)=x﹣4,
∴y=S梯形EMCD﹣S△FDG=CD(DE+CM)﹣![]() DG2=
DG2=![]() ×2×(x﹣2+x)﹣
×2×(x﹣2+x)﹣![]() (x﹣4)2=﹣
(x﹣4)2=﹣![]() x2+6x﹣10,
x2+6x﹣10,
故选项D正确;
故选D.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(﹣1,1),B(0,﹣2),C(1,0),点P(0,2)绕点A旋转180°得到点P1,点P1绕点B旋转180°得到点P2,点P2绕点C旋转180°得到点P3,点P3绕点A旋转180°得到点P4,…,按此作法进行下去,则点P2019的坐标为( )
A.(-2,0)B.![]() C.(2,-4)D.(-2,-2)
C.(2,-4)D.(-2,-2)
查看答案和解析>>
科目:初中数学 来源: 题型:
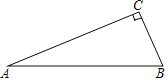
【题目】如图,已知△ABC,且∠ACB=90°.
(1)请用直尺和圆规按要求作图(保留作图痕迹,不写作法和证明):
①以点A为圆心,BC边的长为半径作⊙A;
②以点B为顶点,在AB边的下方作∠ABD=∠BAC.
(2)请判断直线BD与⊙A的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年“五一”假期,某数学活动小组组织一次登山活动.他们从山脚下A点出发沿斜坡AB到达B点,再从B点沿斜坡BC到达山顶C点,路线如图所示.斜坡AB的长为1000米,斜坡BC的长为200![]() 米,在C点测得B点的俯角为45°,已知A点海拔21米,C点海拔721米.
米,在C点测得B点的俯角为45°,已知A点海拔21米,C点海拔721米.
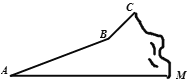
(1)求B点的海拔;
(2)求斜坡AB的坡角.
查看答案和解析>>
科目:初中数学 来源: 题型:
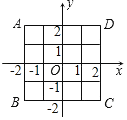
【题目】如图,在直角坐标系中的正方形ABCD边长为4,正方形ABCD的中心为原点O.现做如下实验:抛掷一枚均匀的正方体的骰子(六个面分别标有1至6这六个点数中的一个),每个面朝上的机会是相同的,连续抛掷两次,将骰子朝上的点数作为直角坐标系中点P的坐标(第次的点数作为横坐标,第二次的点数作为纵坐标)
(1)求点P落在正方形ABCD面上(含正方形内部和边界)的概率;
(2)试将正方形ABCD平移整数个单位,则是否存在一种平移,使点P落在正方形ABCD面上的概率为![]() ?若存在,请指出平移方式;若不存在,请说明理由.
?若存在,请指出平移方式;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
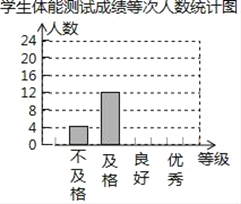
【题目】某校为了解学生体质情况,从各年级随机抽取部分学生进行体能测试,每个学生的测试成绩按标准对应为优秀、良好、及格、不及格四个等级,统计员在将测试数据绘制成图表时发现,优秀漏统计4人,良好漏统计6人,于是及时更正,从而形成如图图表,请按正确数据解答下列各题:
学生体能测试成绩各等次人数统计表
体能等级 | 调整前人数 | 调整后人数 |
优秀 | 8 |
|
良好 | 16 |
|
及格 | 12 |
|
不及格 | 4 |
|
合计 | 40 |
|
(1)填写统计表;
(2)根据调整后数据,补全条形统计图;
(3)若该校共有学生1500人,请你估算出该校体能测试等级为“优秀”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
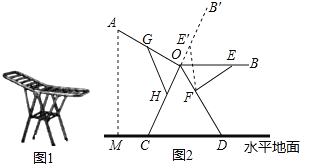
【题目】图1是一种折叠式晾衣架.晾衣时,该晾衣架左右晾衣臂张开后示意图如图2所示,两支脚OC=OD=10分米,展开角∠COD=60°,晾衣臂OA=OB=10分米,晾衣臂支架HG=FE=6分米,且HO=FO=4分米.当∠AOC=90°时,点A离地面的距离AM为_______分米;当OB从水平状态旋转到OB′(在CO延长线上)时,点E绕点F随之旋转至OB′上的点E′处,则B′E′﹣BE为_________分米.
查看答案和解析>>
科目:初中数学 来源: 题型:
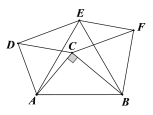
【题目】如图,△ACB中,∠ACB=90°,在AB的同侧分别作正△ACD、正△ABE和正△BCF. 若四边形CDEF的周长是24,面积是17,则AB的长是_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com