练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

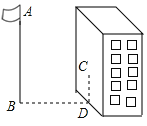
    【题目】如图，在某一时刻测得1米长的竹竿竖直放置时影长1.2米，在同一时刻旗杆AB的影长不全落在水平地面上，有一部分落在楼房的墙上，测得落在地面上的影长BD=9.6米，留在墙上的影长CD=2米，则旗杆的高度AB为____米.

    【答案】10

    【解析】

    根据三个角是直角的四边形是矩形，可得四边形BDCE为矩形，利用矩形的对边相等，可得CE=CE=9.6米，BE=CD=2米，利用“在同一时刻物高与影长的比相等”，可得，从而求出AE的长，继而求出AB的长.

    解：如图，

    过点C作CE⊥AB于点E，可得四边形BDCE为矩形，

    ∴CE=CE=9.6米，BE=CD=2米，

    由题意可得：，

    ∴AE=8(米)，

    ∴AB=AE+BE=8+2=10(米).

    故答案为：10.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

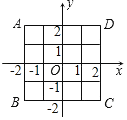
    【题目】如图，在直角坐标系中的正方形ABCD边长为4，正方形ABCD的中心为原点O．现做如下实验：抛掷一枚均匀的正方体的骰子(六个面分别标有1至6这六个点数中的一个)，每个面朝上的机会是相同的，连续抛掷两次，将骰子朝上的点数作为直角坐标系中点P的坐标(第次的点数作为横坐标，第二次的点数作为纵坐标)

    (1)求点P落在正方形ABCD面上(含正方形内部和边界)的概率；

    (2)试将正方形ABCD平移整数个单位，则是否存在一种平移，使点P落在正方形ABCD面上的概率为？若存在，请指出平移方式；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

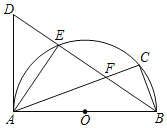
    【题目】如图，以AB为直径作半圆O，点C是半圆上一点，∠ABC的平分线交⊙O于E，D为BE延长线上一点，且DE＝FE．

    （1）求证：AD为⊙O切线；

    （2）若AB＝20，tan∠EBA＝，求BC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校八年级甲、乙两班各有学生50人，为了了解这两个班学生身体素质情况，进行了抽样调查，过程如下，请补充完整．

    （1）收集数据:从甲、乙两个班各随机抽取10名学生进行身体素质测试，测试成绩（百分制）如下：

    甲班65 75 75 80 60 50 75 90 85 65

    乙班90 55 80 70 55 70 95 80 65 70

    （2）整理描述数据:按如下分数段整理、描述这两组样本数据：

    成绩x

    人数

    班级

    50≤x＜60

    60≤x＜70

    70≤x＜80

    80≤x＜90

    90≤x≤100

    甲班

    1

    3

    3

    2

    1

    乙班

    2

    1

    m

    2

    n

    在表中：m=______，n=______．

    （3）分析数据:

    ①两组样本数据的平均数、中位数、众数如表所示：

    班级

    平均数

    中位数

    众数

    甲班

    72

    x

    75

    乙班

    72

    70

    y

    在表中：x=______，y=______．

    ②若规定测试成绩在80分（含80分）以上的学生身体素质为优秀，请估计乙班50名学生中身体素质为优秀的学生有______人．

    ③现从甲班指定的2名学生（1男1女），乙班指定的3名学生（2男1女）中分别抽取1名学生去参加上级部门组织的身体素质测试，用树状图和列表法求抽到的2名同学是1男1女的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

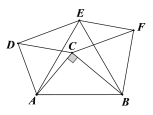
    【题目】如图，△ACB中，∠ACB=90°，在AB的同侧分别作正△ACD、正△ABE和正△BCF. 若四边形CDEF的周长是24，面积是17，则AB的长是_______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有一科技小组进行了机器人行走性能试验，在试验场地有A、B、C三点顺次在同一笔直的赛道上，甲、乙两机器人分别从A、B两点同时同向出发，历时7min同时到达C点，甲机器人前3分钟以a m/min的速度行走，乙机器人始终以60m/min的速度行走，如图是甲、乙两机器人之间的距离y(m)与他们的行走时间x(min)之间的函数图象，请结合图象，回答下列问题：

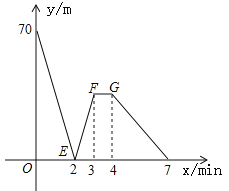
    (1)A、B两点之间的距离是____m，A、C两点之间的距离是____m，a=____m/min；

    (2)求线段EF所在直线的函数解析式；

    (3)设线段FG∥x轴.

    ①当3≤x≤4时，甲机器人的速度为____m/min；

    ②直接写出两机器人出发多长时间相距28m.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①，在平面直角坐标系中，抛物线y=-x2-x-3交x轴于A、B两点(点A在点B的左侧)，交y轴于点C.

    (1)求直线AC的解析式；

    (2)①点P是直线AC上方抛物线上的一个动点(不与点A、点C重合)，过点P作PD⊥AC于点D，求PD的最大值；

    ②当线段PD的长度最大时，点Q从点P出发，先以每秒1个单位长度的速度沿适当的路径运动到y轴上的点M处，再沿MC以每秒个单位长度的速度运动到点C停止，当点Q在整个运动过程中用时最少时，求点M的坐标；

    (3)如图②，将△BOC沿直线BC平移，点B平移后的对应点为点B'，点O平移后的对应点为点O'，点C平移后的对应点为点C'，点S是坐标平面内一点，若以A、C、O'、S为顶点的四边形是菱形，求出所有符合条件的点O'的坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了响应国家有关开展中小学生“课后服务”的政策，某学校课后开设了A：课后作业辅导、B：书法、C：阅读、D：绘画、E：器乐，五门课程供学生选择；其中A（必选项目），再从B、C、D、E中选两门课程．

    （1）若学生小玲第一次选一门课程，直接写出学生小玲选中项目E的概率；

    （2）若学生小强和小明在选项的过程中，第一次都是选了项目E，那么他俩第二次同时选择书法或绘画的概率是多少？请用列表法或画树状图的方法加以说明并列出所有等可能的结果．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明和小刚一起做游戏，游戏规则如下：将分别标有数字 1， 2， 3， 4 的 4 个小球放入一个不透明的袋子中，这些球除数字外都相同．从中随机摸出一个球记下数字后放回，再从中随机摸出一个球记下数字．若两次数字差的绝对值小于 2，则小明获胜，否则小刚获胜．这个游戏对两人公平吗？请说明理由．

    查看答案和解析>>

    同步练习册答案