
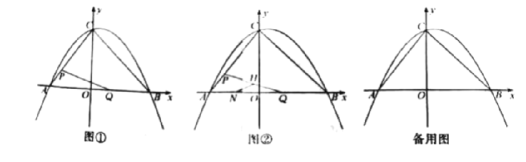
【题目】如图①,在平面直角坐标系中,ニ次函数![]() 的图像与坐标轴交于A,B,C三点,其中点A的坐标为(-3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点0出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ
的图像与坐标轴交于A,B,C三点,其中点A的坐标为(-3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点0出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ
(1)填空:b=_, c=_;
(2)在点P,Q运动过程中,△APQ可能是直角三角形吗?请说明理由;
(3)如图2,点N的坐标为![]() ,线段PQ的中点为H,连接NH,当点Q关于直线NH的对称点Q`恰好落在线段BC上时,请直接写出点Q`的坐标
,线段PQ的中点为H,连接NH,当点Q关于直线NH的对称点Q`恰好落在线段BC上时,请直接写出点Q`的坐标
【答案】(1) ![]() ;(2) △APQ不可能是直角三角形,证明见解析;(3) Q′(
;(2) △APQ不可能是直角三角形,证明见解析;(3) Q′(![]() ,
,![]() ).
).
【解析】
(1)设抛物线的解析式为y=a(x+3)(x-4),将a=![]() 代入可得到抛物线的解析式,从而可确定出b、c的值
代入可得到抛物线的解析式,从而可确定出b、c的值
(2)连结QC.先求得点C的坐标,则PC=5-t,依据勾股定理可求得AC=5,CQ![]() =t
=t![]() +16,接下来,依据CQ
+16,接下来,依据CQ![]() -CP
-CP![]() =AQ
=AQ![]() -AP
-AP![]() 列方程求解即可
列方程求解即可
(3)连结:OP,取OP的中点R,连结RH,NR,延长NR交线段BC与点Q.首先依据三角形的中位线定理得到EH=![]() QO=
QO=![]() t,RH∥OQ,NR=
t,RH∥OQ,NR=![]() AP=
AP=![]() t,则RH=NR,接下来,依据等腰三角形的性质和平行线的性质证明NH是∠QNQ`的平分线,然后求得直线NR和BC的解析式,最后求得直线NR和BC的交点坐标即可
t,则RH=NR,接下来,依据等腰三角形的性质和平行线的性质证明NH是∠QNQ`的平分线,然后求得直线NR和BC的解析式,最后求得直线NR和BC的交点坐标即可
(1)设抛物线的解析式为y=a(+3)(x-4).将a=-![]() 代入得:
代入得:![]()
∴![]()
(2)在点P、Q运动过程中,△APQ不可能是直角三角形。
理由如下:连结QC
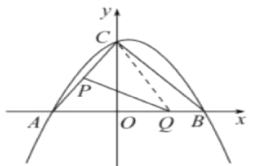
∵在点P、Q运动过程中,∠PAQ、∠PQA始终为锐角,
∴当△APQ是直角三角形时,则∠APQ=90°
将x=0代入抛物线的解析式得:y=4
∴C(0,4)
∵AP=OQ=t
∴PC=5-t
∵在Rt△AOC中,依据勾股定理得:AC=5,在Rt△COQ中,依据勾股定理可知: CQ![]() =t
=t![]() +16,
+16,
在Rt△CPQ中依据勾股定理可知:
PQ![]() =CQ
=CQ![]() -CP
-CP![]() ,在Rt△APQ中,AQ
,在Rt△APQ中,AQ![]() -AP
-AP![]() =PQ
=PQ![]()
∴CQ![]() -CP
-CP![]() =AQ
=AQ![]() -AP
-AP![]() ,即
,即
(3+t)![]() -t
-t![]() =t
=t![]() +16-(5-t)
+16-(5-t)![]() ,解得:t=4.5
,解得:t=4.5
∵由题意可知:0≤t≤4
∴t=4.5不和题意,即△APQ不可能是直角三角形。
(3)如图所示:连结:OP,取OP的中点R,连结RH,NR,延长NR交线段BC与点Q`
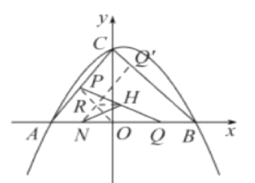
∵点H为PQ的中点,点R为OP的中点
∴EH=![]() QO=
QO=![]() t, RH∥OQ
t, RH∥OQ
∵A(-3,0),N(-![]() ,0)
,0)
∴点N为OA的中点
又∵R为OP的中点,
NR=![]() AP=
AP=![]() t
t
∴RH=NR,
∴∠RNH=∠RHN
∵RH∥OQ,
∴∠RHN=∠HNO
∴∠RNH=∠HNO,即NH是∠QNQ`的平分线.
设直线AC的解析式为y=mx+n,把点A(3,0)、C(0,4)
代入得:![]()
解得: ![]() ,n=4
,n=4
∴直线AC的表示为:y=![]()
同理可求得直线BC的表达式为y=-x+4
设直线NR的函数表达式为y=![]() 将点N的坐标代入得
将点N的坐标代入得![]()
,解得:S=2
直线NR的表述表达式为y=![]()
将直线NR和直线BC的表达式联立得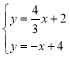
解得:x=![]() , y=
, y=![]() ,
,
∴Q`(![]() ,
,![]() )
)


科目:初中数学 来源: 题型:
【题目】某文明小区50平方米和80平方米两种户型的住宅,50平方米住宅套数是80平方米住宅套数的2倍.物管公司月底按每平方米2元收取当月物管费,该小区全部住宅都人住且每户均按时全额缴纳物管费.
(1)该小区每月可收取物管费90 000元,问该小区共有多少套80平方米的住宅?
(2)为建设“资源节约型社会”,该小区物管公司5月初推出活动一:“垃圾分类送礼物”,50平方米和80平方米的住户分别有40%和20%参加了此次括动.为提离大家的积扱性,6月份准备把活动一升级为活动二:“拉圾分类抵扣物管费”,同时终止活动一.经调査与测算,参加活动一的住户会全部参加活动二,参加活动二的住户会大幅增加,这样,6月份参加活动的50平方米的总户数在5月份参加活动的同户型户数的基础上将增加![]() ,每户物管费将会减少
,每户物管费将会减少![]() ;6月份参加活动的80平方米的总户数在5月份参加活动的同户型户数的基础上将增加
;6月份参加活动的80平方米的总户数在5月份参加活动的同户型户数的基础上将增加![]() ,每户物管费将会减少
,每户物管费将会减少![]() .这样,参加活动的这部分住户6月份总共缴纳的物管费比他们按原方式共缴纳的物管费将减少
.这样,参加活动的这部分住户6月份总共缴纳的物管费比他们按原方式共缴纳的物管费将减少![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
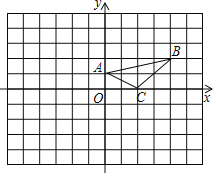
【题目】如图,在平面直角坐标系中,A(0,1),B(4,2),C(2,0).
(1)将△ABC沿y轴翻折得到△A1B1C1,画出△A1B1C1;
(2)将△ABC绕着点(﹣1,﹣1)旋转180°得到△A2B2C2,画出△A2B2C2;
(3)线段B2C2可以看成是线段B1C1绕着平面直角坐标系中某一点逆时针旋转得到,直接写出旋转中心的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,点D为BC边上的一点,点D关于直线AB的对称点为点E,连接AD、DE,在AD上取点F,使得∠EFD=60°,射线EF与AC交于点G.
(1)设∠BAD=α,求∠AGE的度数(用含α的代数式表示);
(2)用等式表示线段CG与BD之间的数量关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某市九年级学生学业考试体育成绩,现从中随机抽取部分学生的体育成绩
进行分段(A:50分;B:49-45分;C:44-40分;D:39-30分;E:29-0分)统计如下:
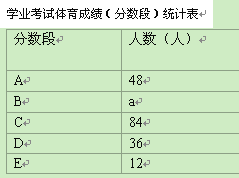
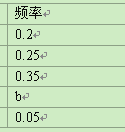
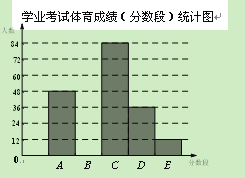
根据上面提供的信息,回答下列问题:
(1)在统计表中,a的值为 ▲ ,b的值为 ▲ ,并将统计图补充完整(温馨提示:作图时别忘了用0.5毫米及以上的黑色签字笔涂黑);
(2)甲同学说:“我的体育成绩是此次抽样调查所得数据的中位数. ”请问:甲同学的体育成绩应在什么分数段内? ▲ (填相应分数段的字母)
(3)如果把成绩在40分以上(含40分)定为优秀,那么该市今年10440名九年级学生中体育成绩为优秀的学生人数约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边△AOC的周长为3,作OD⊥AC于点D,在x轴上取点C1,使CC1=DC,以CC1为边作等边△A1CC1;作CD1⊥A1C1于点D1,在x轴上取点C2,使C1C2=D1C1,以C1C2为边作等边△A2C1C2;作C1D2⊥A2C2于点D2,在x轴上取点C,使C2C3=D2C2,以C2C3为边作等边△A3C2C3;…,且点A,A1,A2,A3,…都在第一象限,如此下去,则等边△A2019C2018C2019的顶点A2019坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+4的图象与x轴交于点A(4,0)和点D(﹣1,0),与y轴交于点C,过点C作BC平行于x轴交抛物线于点B,连接AC
(1)求这个二次函数的表达式;
(2)点M从点O出发以每秒2个单位长度的速度向点A运动;点N从点B同时出发,以每秒1个单位长度的速度向点C运动,其中一个动点到达终点时,另一个动点也随之停动,过点N作NQ垂直于BC交AC于点Q,连结MQ.
①求△AQM的面积S与运动时间t之间的函数关系式,写出自变量的取值范围;当t为何值时,S有最大值,并求出S的最大值;
②是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标;若不存在,说明理由.
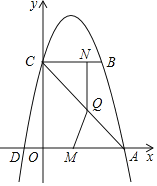
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅行团32人在景区A游玩,他们由成人、少年和儿童组成.已知儿童10人,成人比少年多12人.
(1)求该旅行团中成人与少年分别是多少人?
(2)因时间充裕,该团准备让成人和少年(至少各1名)带领10名儿童去另一景区B游玩.景区B的门票价格为100元/张,成人全票,少年8折,儿童6折,一名成人可以免费携带一名儿童.
①若由成人8人和少年5人带队,则所需门票的总费用是多少元?
②若剩余经费只有1200元可用于购票,在不超额的前提下,最多可以安排成人和少年共多少人带队?求所有满足条件的方案,并指出哪种方案购票费用最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家庭记录了未使用节水龙头50天的日用水量(单位:m3)和使用了节木龙头50天的日用水量,得到频数分布表如下:
表1未使用节水龙头50天的日用水量频数分布表
日用水量x | 0≤x<0.1 | 0.1≤x<0.2 | 0.2≤x<0.3 | 0.3≤x<0.4 | 0.4≤x<0.5 | 0.5≤x<0.6 | 0.6≤x≤0.7 |
频数 | 1 | 3 | 2 | 4 | 9 | 26 | 5 |
表2使用了节水龙头50天的日用水量频数分布表
日用水量x | 0≤x<0.1 | 0.1≤x<0.2 | 0.2≤x<0.3 | 0.3≤x<0.4 | 0.4≤x<0.5 | 0.5≤x<0.6 |
频数 | 1 | 5 | 13 | 10 | 16 | 5 |
(1)估计该家庭使用节水龙头后,日用水量小于0.3 m3的概率;
(2)估计该家庭使用节水龙头后,一年能节省多少水?(一年按365天计算,同一组中的数据以这组数据所在范围的组中值作代表.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com