
����Ŀ����ͼ����֪�ȱߡ�AOC���ܳ�Ϊ3����OD��AC�ڵ�D����x����ȡ��C1��ʹCC1��DC����CC1Ϊ�����ȱߡ�A1CC1����CD1��A1C1�ڵ�D1����x����ȡ��C2��ʹC1C2��D1C1����C1C2Ϊ�����ȱߡ�A2C1C2����C1D2��A2C2�ڵ�D2����x����ȡ��C��ʹC2C3��D2C2����C2C3Ϊ�����ȱߡ�A3C2C3�������ҵ�A��A1��A2��A3�������ڵ�һ���ޣ������ȥ����ȱߡ�A2019C2018C2019�Ķ���A2019����Ϊ_____��

���𰸡�(![]() ��
��![]() )
)
��������
���ݵȱ������ε����ʷֱ����C1C2��C2C3��C3C4������CnCn+1�ı߳����ɽ�����⣮
�ߵȱ���A1C1C2���ܳ�Ϊ3��OD��AC�ڵ�D��
��OC��1��C1C2��CD��![]() OC��
OC��![]() ��
��
��OC��CC1��C1C2��C2C3������C2018C2019�ij��ֱ�Ϊ1��![]() ��
��![]() ��
��![]() ������
������![]() ��
��
OC2019��OC+CC1+C1C2+C2C3����+C2018C2019��1+![]() +
+![]() +
+![]() +��+
+��+![]() ��
��![]() ��
��
�ȱ���A2019C2018C2019����A2019�ĺ����ꣽ![]() ��
��![]() ��
��![]() ��
��
�ȱ���A2019C2018C2019����A2019�������ꣽ![]() ��
��![]() ��
��![]() ��
��
�ʴ�Ϊ��(![]() ��
��![]() )��
)��


 �����Ļ�������ҵϵ�д�
�����Ļ�������ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
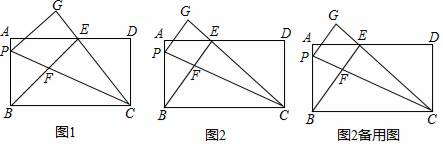
����Ŀ���ھ���ABCD�У�AB=12��P�DZ�AB��һ�㣬����PBC��ֱ��PC�۵�������B�Ķ�Ӧ���ǵ�G������B��BE��CG������ΪE����AD�ϣ�BE��PC�ڵ�F��
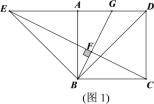
��1����ͼ1������E��AD���е㣬��֤����AEB�ա�DEC��
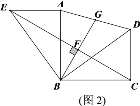
��2����ͼ2������֤��BP=BF��
�ڵ�AD=25����AE��DEʱ����cos��PCB��ֵ��
�۵�BP=9ʱ����BEEF��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺����������һ���е㣬��ƽ���������ܳ���ֱ�߽�������������ڸñ��ϵ��з��ߣ����������������ڲ��IJ��ֽ����з��߶Σ�
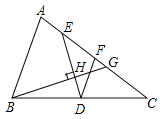
��1����ͼ����ABC�У�AC��AB��DE�ǡ�ABC��BC���ϵ��з��߶Σ�FΪAC�е㣬����B��DE�Ĵ��߽�AC�ڵ�G������ΪH����AC��b��AB��c��
����֤��DF��EF��
����b��6��c��4����CG�ij��ȣ�
��2�����⣨1���У�S��BDH��S��EGH����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
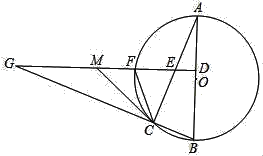
����Ŀ����ͼ���ڡ�O�У�ABΪֱ����ACΪ�ң���BC�ӳ�����һ��G����GD��AO�ڵ�D����AC�ڵ�E������O�ڵ�F��M��GE���е㣬����CF��CM��
��1���ж�CM���O��λ�ù�ϵ����˵�����ɣ�
��2������ECF=2��A��CM=6��CF=4����MF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
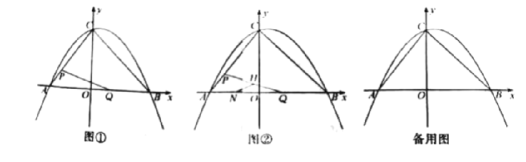
����Ŀ����ͼ��,��ƽ��ֱ������ϵ��,�˴κ���![]() ��ͼ���������ύ��A,B,C����,���е�A������Ϊ(-3,0),��B������Ϊ(4,0),����AC,BC.����P�ӵ�A����,���߶�AC����ÿ��1����λ���ȵ��ٶ����C�������˶�;ͬʱ,����Q�ӵ�0����,���߶�OB����ÿ��1����λ���ȵ��ٶ����B�������˶�,������һ�㵽���յ�ʱ,��һ����ֹ֮ͣ�˶�,���˶�ʱ��Ϊt��.����PQ
��ͼ���������ύ��A,B,C����,���е�A������Ϊ(-3,0),��B������Ϊ(4,0),����AC,BC.����P�ӵ�A����,���߶�AC����ÿ��1����λ���ȵ��ٶ����C�������˶�;ͬʱ,����Q�ӵ�0����,���߶�OB����ÿ��1����λ���ȵ��ٶ����B�������˶�,������һ�㵽���յ�ʱ,��һ����ֹ֮ͣ�˶�,���˶�ʱ��Ϊt��.����PQ
��1�����:b=_, c=_;
��2���ڵ�P,Q�˶�������,��APQ������ֱ����������?��˵������;
��3����ͼ2,��N������Ϊ![]() ,�߶�PQ���е�ΪH,����NH,����Q����ֱ��NH�ĶԳƵ�Q`ǡ�������߶�BC��ʱ,��ֱ��д����Q`������
,�߶�PQ���е�ΪH,����NH,����Q����ֱ��NH�ĶԳƵ�Q`ǡ�������߶�BC��ʱ,��ֱ��д����Q`������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
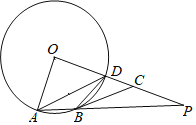
����Ŀ����ͼ����֪OA�ǡ�O�İ뾶��ABΪ��O���ң�����O��OP��OA����AB���ӳ�����һ��P��OP����O�ڵ�D������AD��BD������B����O������BC��OP�ڵ�C
(1)��֤����CBP����ADB��
(2)��O4��4��AB��2�����߶�BP�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���Ų��õ���б�������ͣ����ͼ����ͼ���Ǵ�ͼ���������ƽ��ͼ��������վ�����ϲ������AB��ˮƽ����ļн���30�㣬����CD��ˮƽ����ļн���60�㣬���������˵ľ���BCΪ2�ף��������˾���ADΪ20�ף����������BH�ij����������ȷ��0.1�ף� ![]() ��1.73��
��1.73��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǰ�ԲO��ֱ������AB=12����CΪ��Բ�ϵ�һ�㣮���˰�Բ��BC���ڵ�ֱ���۵�����Բ��BCǡ�ù�Բ��O����ͼ����Ӱ���ֵ�����ǣ�������

A. 4��B. 5��C. 6��D. 8��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У�CD��AB����ABC=90����AB=BC������BCD�Ƶ�B��ʱ����ת90���õ���BAE������CE������B��BG��CE�ڵ�F����AD�ڵ�G.
(1)��ͼ1��CD=AB.
����֤���ı���ABCD�������Σ�
����֤��G��AD�е㣻
(2)��ͼ2����CD<AB�����ж�G�Ƿ���Ȼ��AD���е�?���ǣ���֤���������ǣ���˵����.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com