
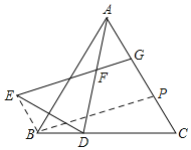
【题目】如图,在等边三角形ABC中,点D为BC边上的一点,点D关于直线AB的对称点为点E,连接AD、DE,在AD上取点F,使得∠EFD=60°,射线EF与AC交于点G.
(1)设∠BAD=α,求∠AGE的度数(用含α的代数式表示);
(2)用等式表示线段CG与BD之间的数量关系,并证明.

【答案】(1)60°+α;(2)CG=2BD,证明见解析.
【解析】
(1)根据等边三角形的性质和三角形的内角和定理可得结论;
(2)作辅助线,构建全等三角形,证明四边形EBPG是平行四边形,得BE=PG,再证明△ABD≌△BCP(AAS),可得结论.
解:(1)∵△ABC是等边三角形,
∴∠BAC=60°,
∵∠BAD=α,
∴∠FAG=60°-α,
∵∠AFG=∠EFD=60°,
∴∠AGE=180°-60°-(60°-α)=60°+α;
(2)CG=2BD,理由是:
如图,连接BE,过B作BP∥EG,交AC于P,则∠BPC=∠EGP,
∵点D关于直线AB的对称点为点E,
∴∠ABE=∠ABD=60°,
∵∠C=60°,
∴∠EBD+∠C=180°,
∴EB∥GP,
∴四边形EBPG是平行四边形,
∴BE=PG,
∵∠DFG+∠C=120°+60°=180°,
∴∠FGC+∠FDC=180°,
∴∠ADB=∠BGP=∠BPC,
∵AB=BC,∠ABD=∠C=60°,
∴△ABD≌△BCP(AAS),
∴BD=PC=BE=PG,
∴CG=2BD.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:
【题目】某图书馆计划选购甲、乙两种图书.已知甲图书每本价格是乙图书每本价格的2.5倍,用800元单独购买甲图书比用800元单独购买乙图书要少24本.
(1)甲、乙两种图书每本价格分别为多少元?
(2)如果该图书馆计划购买乙图书的本数比购买甲图书本数的2倍多8本,且用于购买甲、乙两种图书的总经费不超过1060元,那么该图书馆最多可以购买多少本乙图书?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】央视“经典咏流传”开播以来受到社会广泛关注,我市也在各个学校开展了传承经典的相关主题活动“戏曲进校园”.某校对此项活动的喜爱情况进行了随机调查,对收集的信息进行统计,绘制了下面两副尚不完整的统计图,请你根据统计图所提供的信息解答下列问题:
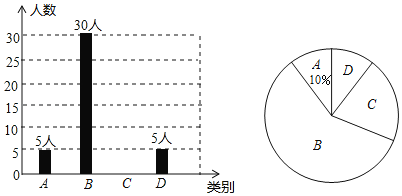
图中A表示“很喜欢”,B表示“喜欢”,C表示“一般”,D表示“不喜欢”.
(1)被调查的总人数是 人,扇形统计图中B部分所对应的扇形圆心角的度数为 ,并补全条形统计图;
(2)若该校共有学生1800人,请根据上述调查结果估计该校学生中A类有多少人;
(3)在A类5人中,刚好有3个女生2个男生,从中随机抽取两个同学担任两角色,用树状图或列表法求出被抽到的两个学生性别相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:经过三角形一边中点,且平分三角形周长的直线叫做这个三角形在该边上的中分线,其中落在三角形内部的部分叫做中分线段.
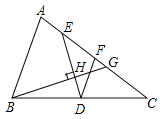
(1)如图,△ABC中,AC>AB,DE是△ABC在BC边上的中分线段,F为AC中点,过点B作DE的垂线交AC于点G,垂足为H,设AC=b,AB=c.
①求证:DF=EF;
②若b=6,c=4,求CG的长度;
(2)若题(1)中,S△BDH=S△EGH,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
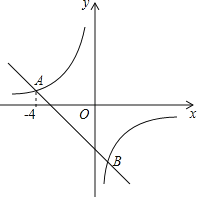
【题目】在平面直角坐标系xOy中,一次函数y=-x+k的图象与反比例函数y=-![]() 的图象交于点A(-4,n)和点B.
的图象交于点A(-4,n)和点B.
(1)求k的值和点B的坐标;
(2)若P是x轴上一点,且AP=AB,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
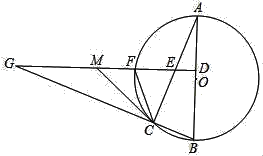
【题目】如图,在⊙O中,AB为直径,AC为弦.过BC延长线上一点G,作GD⊥AO于点D,交AC于点E,交⊙O于点F,M是GE的中点,连接CF,CM.
(1)判断CM与⊙O的位置关系,并说明理由;
(2)若∠ECF=2∠A,CM=6,CF=4,求MF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
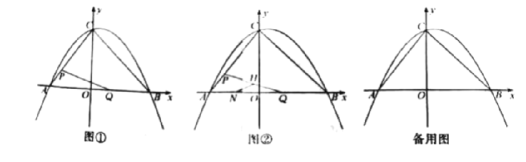
【题目】如图①,在平面直角坐标系中,ニ次函数![]() 的图像与坐标轴交于A,B,C三点,其中点A的坐标为(-3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点0出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ
的图像与坐标轴交于A,B,C三点,其中点A的坐标为(-3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点0出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ
(1)填空:b=_, c=_;
(2)在点P,Q运动过程中,△APQ可能是直角三角形吗?请说明理由;
(3)如图2,点N的坐标为![]() ,线段PQ的中点为H,连接NH,当点Q关于直线NH的对称点Q`恰好落在线段BC上时,请直接写出点Q`的坐标
,线段PQ的中点为H,连接NH,当点Q关于直线NH的对称点Q`恰好落在线段BC上时,请直接写出点Q`的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2米,两拉索底端距离AD为20米,请求出立柱BH的长.(结果精确到0.1米, ![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
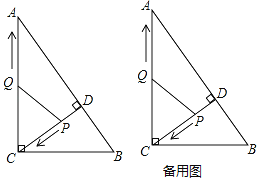
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D,点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.
(1)求线段CD的长;
(2)当△CPQ与△BDC相似时,求t值;
(3) 设△CPQ的面积为y,求y与t的函数关系式,并判断△PCQ的面积是否有最大值还是最小值?若有,求出t为何值时y的最值,若没有,则说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com