
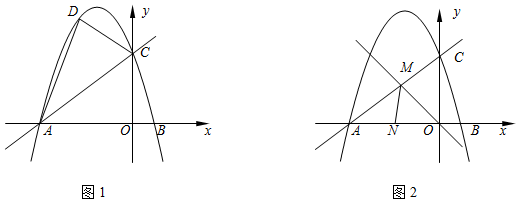
分析 (1)根据直线y=$\frac{3}{4}$x+6,可得A(-8,0),C(0,6),设抛物线解析式为y=a(x+8)(x-2),把C(0,6)代入,可得抛物线的函数关系式;
(2)过P作PH⊥AO于H,根据S△PCD=2S△PAD,可得AP:PC=1:2,即AH:HO=1:2,进而得到OH=$\frac{2}{3}$AO=8×$\frac{2}{3}$=$\frac{16}{3}$,在直线y=$\frac{3}{4}$x+6中,当x=$-\frac{16}{3}$时,y=$\frac{3}{4}$×($-\frac{16}{3}$)+6=2,可得点P的坐标为($-\frac{16}{3}$,2);
(3)分两种情况进行讨论:①当点Q1为∠NMO的平分线与x轴的交点时,点Q1到直线MN和直线MO的距离相等;②当点Q2为∠NMO的邻补角的平分线与x轴的交点时,点Q2到直线MN和直线MO的距离相等,根据相似三角形的性质求得N(-$\frac{192}{49}$,0),再根据角平分线的性质可得点Q1的坐标为($-\frac{16}{7}$,0);最后根据MQ1⊥MQ2,可得直线MQ2解析式为y=$\frac{1}{3}$x+$\frac{32}{7}$,进而得到点Q2的坐标为($-\frac{96}{7}$,0).
解答 解:(1)在y=$\frac{3}{4}$x+6中,
令x=0,则y=6;令y=0,则x=-8,
∴A(-8,0),C(0,6),
∵点B的横坐标为2,
∴B(2,0),
设抛物线解析式为y=a(x+8)(x-2),则
把C(0,6)代入,得6=a×(-16),
∴a=-$\frac{3}{8}$,
∴y=-$\frac{3}{8}$(x+8)(x-2),
即$y=-\frac{3}{8}{x^2}-\frac{9}{4}x+6$;
(2)如图所示,过P作PH⊥AO于H,
∵S△PCD=2S△PAD,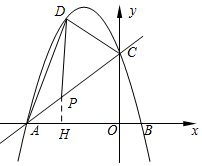
∴AP:PC=1:2,
∵PH∥CO,
∴AH:HO=1:2,
即OH=$\frac{2}{3}$AO,
又∵AO=8,
∴OH=8×$\frac{2}{3}$=$\frac{16}{3}$,
∴点P的横坐标为$-\frac{16}{3}$,
在直线y=$\frac{3}{4}$x+6中,当x=$-\frac{16}{3}$时,y=$\frac{3}{4}$×($-\frac{16}{3}$)+6=2,
∴点P的纵坐标为2,
∴点P的坐标为($-\frac{16}{3}$,2);
(3)分两种情况:
①当点Q1为∠NMO的平分线与x轴的交点时,点Q1到直线MN和直线MO的距离相等,
∵直线y=-x与直线y=$\frac{3}{4}$x+6交于点M,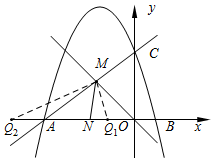
∴M(-$\frac{24}{7}$,$\frac{24}{7}$),
又∵A(-8,0),
∴由两点间距离公式可得AM=$\sqrt{(-\frac{24}{7}+8)^{2}+(\frac{24}{7})^{2}}$=$\frac{40}{7}$,
∵∠AMN=∠AOM,∠MAN=∠OAM,
∴△AMN∽△AOM,
∴AM2=AN×AO,即($\frac{40}{7}$)2=AN×8,
∴AN=$\frac{200}{49}$,
∴ON=AO-AN=$\frac{192}{49}$,
即N(-$\frac{192}{49}$,0),
∴由两点间距离公式可得MN=$\frac{120}{49}\sqrt{2}$,MO=$\frac{24}{7}\sqrt{2}$,
∵MQ1平分∠NMO,
∴$\frac{O{Q}_{1}}{N{Q}_{1}}$=$\frac{MO}{MN}$=$\frac{7}{5}$,
∴OQ1=$\frac{7}{12}$NO=$\frac{7}{12}×\frac{192}{49}$=$\frac{16}{7}$,
即点Q1的坐标为($-\frac{16}{7}$,0);
②当点Q2为∠NMO的邻补角的平分线与x轴的交点时,点Q2到直线MN和直线MO的距离相等,
根据Q1($-\frac{16}{7}$,0),M(-$\frac{24}{7}$,$\frac{24}{7}$),可得
直线MQ1解析式为y=-3x-$\frac{48}{7}$,
∵MQ1⊥MQ2,
∴可设直线MQ2解析式为y=$\frac{1}{3}$x+b,
把M(-$\frac{24}{7}$,$\frac{24}{7}$)代入,可得b=$\frac{32}{7}$,
∴直线MQ2解析式为y=$\frac{1}{3}$x+$\frac{32}{7}$,
∴当y=0时,0=$\frac{1}{3}$x+$\frac{32}{7}$,
解得x=-$\frac{96}{7}$,
即点Q2的坐标为($-\frac{96}{7}$,0).
综上所述,点Q的坐标为($-\frac{16}{7}$,0)或($-\frac{96}{7}$,0).
点评 本题属于二次函数综合题,主要考查了待定系数法求函数解析式,角平分线的性质,平行线分线段成比例定理,相似三角形的判定与性质以及两点间的距离公式的综合应用,解决问题的关键是运用两点间距离公式求得线段的长,运用分类思想进行求解.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
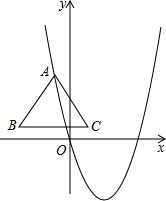 如图,已知等边三角形ABC的边长为$2\sqrt{3}$,它的顶点A在抛物线y=x2-2$\sqrt{3}$x上运动,且始终使BC∥x轴.
如图,已知等边三角形ABC的边长为$2\sqrt{3}$,它的顶点A在抛物线y=x2-2$\sqrt{3}$x上运动,且始终使BC∥x轴.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (3a+b)(3b-a) | B. | ($\frac{1}{3}$x-1)(1+$\frac{1}{3}$x) | C. | (2x-y)(-2x+y) | D. | (-s-t)(-s-t) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
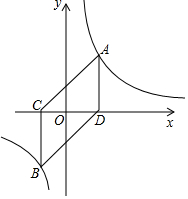 如图,O为坐标原点,点A在第一象限,且在函数y=$\frac{2}{x}$的图象上.延长AO,交双曲线于另一点B,过点A作AD⊥x轴于点D,过点B作BC⊥x轴于点C,连接AC、BD.(注:不能用双曲线关于原点对称解答下列问题)
如图,O为坐标原点,点A在第一象限,且在函数y=$\frac{2}{x}$的图象上.延长AO,交双曲线于另一点B,过点A作AD⊥x轴于点D,过点B作BC⊥x轴于点C,连接AC、BD.(注:不能用双曲线关于原点对称解答下列问题)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com