
分析 (1)根据“互为相反数的绝对值相等”,即可解答;
(2)根据ab>0,bc<0得到a=5,b=1,c=-2或a=-5,b=-1,c=4,然后把两组分别代入代数式计算即可.
解答 解:(1)∵|a|=5,|b|=1,|c-1|=3.
∴a=±5,b=±1,c=4或-2,
故答案为:±5,±1,4或-2;
(2)∵ab>0,bc<0,a=±5,b=±1,c=4或-2,
∴a=5,b=1,c=-2,或a=-5,b=-1,c=4,
∴ab-bc-ca=5×1-1×(-2)-(-2)×5=5+2+10=17或ab-bc-ca=-5×(-1)-(-1)×4-4×(-5)=5+4+20=29.
点评 本题考查了绝对值,解决本题的关键是熟记绝对值的定义.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -8、-10 | B. | -8、10 | C. | 8、-10 | D. | 8、10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
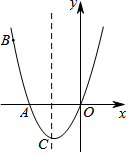 如图,已知抛物线C1经过A(-2,0),B(-3,3)及原点O,顶点为C.
如图,已知抛物线C1经过A(-2,0),B(-3,3)及原点O,顶点为C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2-x}$ | B. | $\sqrt{x-2}$ | C. | -$\sqrt{2-x}$ | D. | -$\sqrt{x-2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
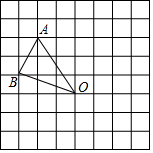 在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABO的三个顶点都在格点上.
在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABO的三个顶点都在格点上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com