
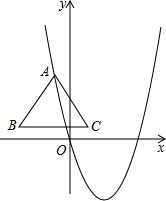
 ��ͼ����֪�ȱ�������ABC�ı߳�Ϊ$2\sqrt{3}$�����Ķ���A��������y=x2-2$\sqrt{3}$x���˶�����ʼ��ʹBC��x�ᣮ
��ͼ����֪�ȱ�������ABC�ı߳�Ϊ$2\sqrt{3}$�����Ķ���A��������y=x2-2$\sqrt{3}$x���˶�����ʼ��ʹBC��x�ᣮ���� ��1��������A�˶�����ԭ���غ�ʱ����BC��y�ύ�ڵ�D����ͼ��ʾ���ɵȱ������ε����ʿ������AD��ֵ���Ӷ����C�����꣮
��2������A��AD��BC�ڵ�D�����A������꣬��������ʾ��AD��ֵ���������Ǻ������AD��ֵ���Ӷ�����������ϵ���Ϳ������A�����꣮
��3��B�������������������������B����x����ʱ����A��������Ϊ3�����������ߵĽ���ʽ���A�ĺ�����Ϳ������C�����ꣻ��B��y����ʱ���������A��ĺ�����$\sqrt{3}$�����������ߵĽ���ʽ�������A��������꣬�Ӷ����C������꣮
��� 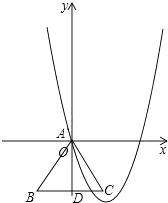 �⣺��1��������A�˶�����ԭ���غ�ʱ����BC��y�ύ�ڵ�D����ͼ��ʾ��
�⣺��1��������A�˶�����ԭ���غ�ʱ����BC��y�ύ�ڵ�D����ͼ��ʾ��
��BC��x�ᣬBC=AC=2$\sqrt{3}$��
��CD=$\sqrt{3}$��AD=3��
��C���������$\sqrt{3}$��-3����
�ߵ�x=$\sqrt{3}$ʱ��y=��$\sqrt{3}$��2-2$\sqrt{3}$��$\sqrt{3}$=-3��
�൱����A�˶�����ԭ���غ�ʱ������C���������ϣ�
��2������A��AD��BC�ڵ�D��
���A��������x��x2-2$\sqrt{3}$x����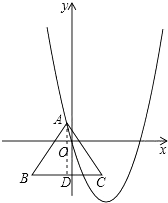
��BC��x�ᣬ
��x���ϲ��ֵ������Ρס�ABC��
��S����S��=1��8��
��S����S��ABC=1��9��
��AD=3��x2-2$\sqrt{3}$x����
�ߵȱߡ�ABC�ı߳�Ϊ2$\sqrt{3}$��
��AD=AC•sin60��=3��
��3��x2-2$\sqrt{3}$x��=3��
��x2-2$\sqrt{3}$x-1=0��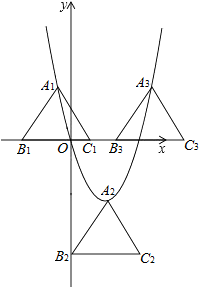
�ⷽ�̣��� x=$\sqrt{3}$��2��
�ඥ��A������Ϊ��$\sqrt{3}$+2��1����$\sqrt{3}$-2��1����
��3��������B����x��ʱ����A��������Ϊ3��
��3=x2-2$\sqrt{3}$x��
��x=$\sqrt{3}$-$\sqrt{6}$��$\sqrt{3}$+$\sqrt{6}$��
�ඥ��C������Ϊ��2$\sqrt{3}$-$\sqrt{6}$��0������2$\sqrt{3}$+$\sqrt{6}$��0����
������B����y��ʱ����A�������Ϊ$\sqrt{3}$��
��y=x2-2$\sqrt{3}$x=-3��
�ඥ��C������Ϊ��2$\sqrt{3}$��-6����
��������������C��������2$\sqrt{3}$-$\sqrt{6}$��0������2$\sqrt{3}$+$\sqrt{6}$��0������2$\sqrt{3}$��-6����
���� ������һ�����κ������ۺ����⣬�����˵�����꣬�����ε�������ȱ������ε����ʣ����������ε��ж������ʵ��ۺ�Ӧ�ã�����������ؼ������ڽ���������ת��Ϊ�������⣬�������ü���ͼ�ε��й����ʡ������Ͷ��κ�����֪ʶ����ע���ھ���Ŀ�е�һЩ����������


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ�Ƕ��κ���y=ax2+bx+c��a��0��ͼ���һ���֣�ֱ��x=-1�ǶԳ��ᣬ�������жϣ���b-2a=0����4a-2b+c��0����a-b+c=-9a��������-3��y1������$\frac{3}{2}$��y2�����������ϵ����㣬��y1��y2��������ȷ���ǣ�������
��ͼ��ʾ�Ƕ��κ���y=ax2+bx+c��a��0��ͼ���һ���֣�ֱ��x=-1�ǶԳ��ᣬ�������жϣ���b-2a=0����4a-2b+c��0����a-b+c=-9a��������-3��y1������$\frac{3}{2}$��y2�����������ϵ����㣬��y1��y2��������ȷ���ǣ�������| A�� | �٢ڢ� | B�� | �٢� | C�� | �٢� | D�� | �٢ۢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪����ͼ���߶�AB=10��C��AB���е㣮
��֪����ͼ���߶�AB=10��C��AB���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
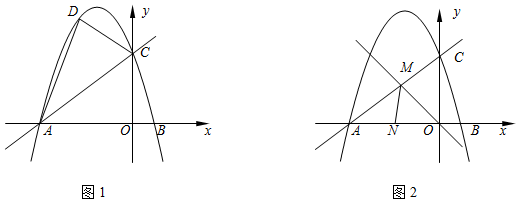
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0.2��0.3��0.4 | B�� | 1��1��2 | C�� | 6��6��6 | D�� | 3��4��5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
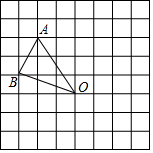 ����ͼ��ʾ�ķ���ֽ�У�ÿ��С�����DZ߳�Ϊ1����λ�������Σ���ABO���������㶼�ڸ���ϣ�
����ͼ��ʾ�ķ���ֽ�У�ÿ��С�����DZ߳�Ϊ1����λ�������Σ���ABO���������㶼�ڸ���ϣ��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com