
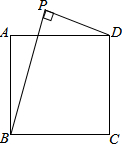
 如图,在正方形ABCD中,CD=$\sqrt{2}$,若在线段AD上方有一点P,满足PD=1,且∠BPD=90°,则点A到BP的距离为( )
如图,在正方形ABCD中,CD=$\sqrt{2}$,若在线段AD上方有一点P,满足PD=1,且∠BPD=90°,则点A到BP的距离为( )| A. | $\frac{\sqrt{3}-1}{2}$ | B. | $\frac{\sqrt{3}+1}{2}$ | ||
| C. | $\frac{\sqrt{3}}{2}$ | D. | 条件不足,无法计算 |
分析 以D为圆心1为半径作⊙D,过点B作⊙D的切线BP、BP′,连接BD,作AE⊥BP′于E,AF⊥BP于F.求出BE、AF即可解决问题.
解答 解:
以D为圆心1为半径作⊙D,过点B作⊙D的切线BP、BP′,连接BD,作AE⊥BP′于E,AF⊥BP于F.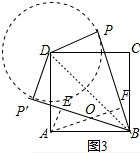
∵四边形ABCD是正方形,CD=BC=AB=AD=$\sqrt{2}$,
∴BD=$\sqrt{2}$DC=2,∠ABC=90°,
在Rt△PBD中,∵∠BPD=90°,BD=2,DP=1,
∴∠PBD=30°,同理∠P′BD=30°,
∴∠ABE=∠CBP=15°,
在△ABE和△BAF中,
$\left\{\begin{array}{l}{∠AEB=∠AFB}\\{∠EAB=∠FBA=75°}\\{AB=BA}\end{array}\right.$,
∴△ABE≌△BAF,
∴∠ABE=∠OAB=15°,
∴∠AOE=∠FOB=30°,
∴AO=OB=2AE,设AE=a,则AO=OB=2a,EO=$\sqrt{3}$a,
∴EB=AF=2a+$\sqrt{3}$a,
∵AB2=AE2+BE2,
∴2=a2+(2a+$\sqrt{3}$a)2,
∴a=$\frac{\sqrt{3}-1}{2}$(负根已经舍弃),
∴AE=$\frac{\sqrt{3}-1}{2}$,AF=BE=2a+$\sqrt{3}$a=$\frac{\sqrt{3}+1}{2}$.
∵点P在线段AD上方,
∴点A到BP的距离=$\frac{\sqrt{3}-1}{2}$
∴故选A.
点评 本题考查四边形综合题、全等三角形的判定和性质、等腰三角形的判定和性质、勾股定理、圆等知识,解题的关键是灵活运用这些知识,学会利用圆的切线的性质解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:选择题
 如图,跷跷板AB的支柱OD经过它的中点O,且垂直于地面BC,垂足为D,OD=50cm,当它的一端B着地时,另一端A离地面的高度AC为( )
如图,跷跷板AB的支柱OD经过它的中点O,且垂直于地面BC,垂足为D,OD=50cm,当它的一端B着地时,另一端A离地面的高度AC为( )| A. | 25cm | B. | 50cm | C. | 75cm | D. | 100cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
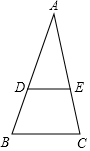 将下列求解过程的理由补充完整.如图,∠ADE=60°,∠B=60°,∠C=80°,求∠AED的度数.解:∵∠ADE=∠B=60°已知
将下列求解过程的理由补充完整.如图,∠ADE=60°,∠B=60°,∠C=80°,求∠AED的度数.解:∵∠ADE=∠B=60°已知查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com