
����Ŀ��ij��˾�ƻ������ס������ֹ��ĵ��ԣ���������ֵ���3̨�����ֵ���2̨�������ʽ�23000Ԫ����������ֵ���4̨�����ֵ���3̨�������ʽ�32000Ԫ��
��1���ס������ֵ���ÿ̨�ļ۸�ֱ��Ƕ���Ԫ��
��2������˾�ƻ����������ֹ��ĵ��Թ�20̨�����м��ֵ��Ե��������������ֵ��Ե���������˾�����ܹ��ṩ������Ե��ʽ�92000Ԫ������Ƽ��ֹ����������˾ѡ��
���𰸡���1����ÿ̨5000Ԫ����ÿ̨4000Ԫ����2�����������֣�����10̨������10̨������11̨������9̨������12̨������8̨��
��������
��1����ס������ֵ���ÿ̨�۸�ֱ�ΪxԪ��yԪ�����������г������飬���������Ľ⼴�ɣ�
��2������ֵ���aԪ�������ֵ��ԣ�20-a��̨�����������г�����ʽ�飬�������ʽ��Ľ⼯���ɣ�
�⣺��1����ס������ֵ���ÿ̨�۸�ֱ�ΪxԪ��yԪ��
![]() ��
��
��ã�![]() ��
��
�𣺼�ÿ̨5000Ԫ����ÿ̨4000Ԫ��
��2������ֵ���aԪ�������ֵ��ԣ�20��a��̨��
![]() ��
��
��ã�10��a��12��
���������֣�����10̨������10̨
����11̨������9̨
����12̨������8̨��


 Ӧ�����������Ĵ���ѧ������ϵ�д�
Ӧ�����������Ĵ���ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ijС������ʹ�ù������������������ij�о�С������ɷø�С����10λ���õ���10λ����һ����ʹ�ù��������Ĵ���ͳ�����£�
ʹ�ô��� | 0 | 5 | 10 | 15 | 20 |
���� | 1 | 1 | 4 | 3 | 1 |
��1����10λ����һ����ʹ�ù���������������λ������ ���Σ��������� ���Σ�ƽ�������� ���Σ�
��2����С��ͬѧ��������20����������30������ô��λ����������ƽ�����в���Ӱ������� ������������λ������������������ƽ��������
��3������С����200�������Թ��Ƹ�С������һ����ʹ�ù����������ܴ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
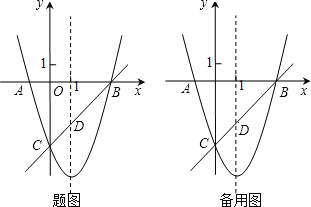
����Ŀ����ͼ����֪������y=x2��bx��c��x�ύ��A��B���㣨A����B����ࣩ����y�ύ�ڵ�C��0����3�����Գ�����ֱ��x=1��ֱ��BC�������ߵĶԳ��ύ�ڵ�D��
��1���������ߵĺ�������ʽ��
��2����ֱ��BC�ĺ�������ʽ��
��3����EΪy����һ���㣬CE�Ĵ�ֱƽ���߽�CE�ڵ�F������������P��Q���㣬�ҵ�P�ڵ������ޣ�
�ٵ��߶�PQ=![]() ABʱ����tan��CED��ֵ��
ABʱ����tan��CED��ֵ��
�ڵ��Ե�C��D��EΪ�������������ֱ��������ʱ����ֱ��д����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������ABCD�Ķ���A���������ֱ��AP����B����ֱ��AP�ĶԳƵ�ΪE������BE��DE������DE��ֱ��AP�ڵ�F��
��1�������ⲹȫͼ1��
��2������PAB��30�㣬���ADF�Ķ�����
��3����ͼ����45�㣼��PAB��90�㣬�õ�ʽ��ʾ�߶�AB��FE��FD֮���������ϵ����֤����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
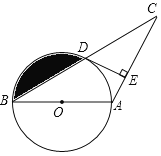
����Ŀ����֪����ͼ������ABC�У�AB��AC����ABΪֱ���ġ�O��BC�ڵ�D������D��DE��AC�ڵ�E��
��1����֤��DE�ǡ�O�����ߣ�
��2������O�İ뾶Ϊ3cm����C��30������ͼ����Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB����O��ֱ����CD���ң�AB��CD������ΪE����P����O�ϣ�����BP��PD��BC����CD=![]() ��sinP=
��sinP=![]() ������O��ֱ��Ϊ��������
������O��ֱ��Ϊ��������

A. 8 B. 6 C. 5 D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(��С������8��)
�Ķ����ϣ�
��ͼ,���ı���ABCD�У��Խ���AC��BD������ΪP.
��֤��S�ı���ABCD=![]()
֤����AC��BD��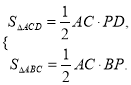
��S�ı���ABCD=S��ACD+S��ACB= ![]()
=![]()
������⣺
��1������֤���õ������ʿ�����Ϊ_______________________________________.
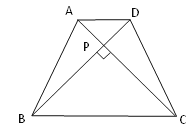
��2����֪����ͼ����������ABCD�У�AD��BC���Խ���AC��BD���ཻ�ڵ�P��AD=3cm,BC=7cm���������������������ε����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У��ֽ�һ�����ֱ�����ǰ�ABC���ڵڶ����ޣ�б�������������ϣ���CΪ (��1��0)����ͼ17��ʾ��B����������![]() ͼ���ϣ�����B��BD��x�ᣬ����ΪD����B�������Ϊ��3��
ͼ���ϣ�����B��BD��x�ᣬ����ΪD����B�������Ϊ��3��
��1����֤����BDC�ա�COA��
��2����BC����ֱ�ߵĺ�����ϵʽ��
��3�������ߵĶԳ������Ƿ���ڵ�P��ʹ��ACP����ACΪֱ�DZߵ�ֱ�������Σ������ڣ�������е�P�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
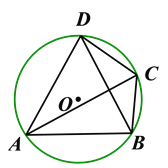
����Ŀ����ͼ���ڡ�O���ڽ��ı���ABCD�У���BCD=120����ACƽ�֡�BCD.
(1)��֤����ABD�ǵȱ������Σ�
(2)��BD=6cm�����O�İ뾶.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com