
【题目】在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上,点C为 (-1,0).如图17所示,B点在抛物线![]() 图象上,过点B作BD⊥x轴,垂足为D,且B点横坐标为-3.
图象上,过点B作BD⊥x轴,垂足为D,且B点横坐标为-3.
(1)求证:△BDC≌△COA;
(2)求BC所在直线的函数关系式;
(3)抛物线的对称轴上是否存在点P,使△ACP是以AC为直角边的直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.

【答案】(1)见解析;(2)![]() (3)存在,P1(
(3)存在,P1(![]() ,
,![]() )、P2(
)、P2(![]() ,
,![]() )
)
【解析】
(1)由等腰直角三角形的性质,平角定义,直角三角形两锐角的关系,可由AAS证得。
(2)求出点B的坐标,由点B、C的坐标,用待定系数法可求BC所在直线的函数关系式。
(3)分点C为直角顶点和点A为直角顶点两种情况讨论即可。
解:(1)证明:∵∠BCD+∠ACO=90°,∠ACO+∠OAC=90°,
∴∠BCD=∠OAC。
∵△ABC为等腰直角三角形 ,∴BC=AC。
在△BDC和△COA中,∠BDC=∠COA=90°,∠BCD=∠OAC,BC=AC,
∴△BDC≌△COA(AAS)。
(2)∵C点坐标为 (-1,0),∴BD=CO=1。
∵B点横坐标为-3,∴B点坐标为 (-3,1)。
设BC所在直线的函数关系式为y=kx+b,
∴![]() ,解得
,解得![]() 。∴BC所在直线的函数关系式为y=-
。∴BC所在直线的函数关系式为y=-![]() x-
x-![]() 。
。
(3)存在 。
∵y=![]() x2+
x2+![]() x-2=
x-2=![]() (x+
(x+![]() )2x-
)2x-![]() ,∴对称轴为直线x=-
,∴对称轴为直线x=-![]() 。
。
若以AC为直角边,点C为直角顶点,对称轴上有一点P1,使CP1⊥AC,
∵BC⊥AC,∴点P1为直线BC与对轴称直线x=-![]() 的交点。
的交点。
由题意可得:![]() , 解得,
, 解得,![]() 。∴P1(-
。∴P1(-![]() ,-
,-![]() )。
)。
若以AC为直角边,点A为直角顶点,对称轴上有一点P2,使AP2⊥AC,
则过点A作A P2∥BC,交对轴称直线x=-![]() 于点P2,
于点P2,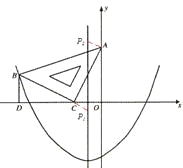
∵CD=OA,∴A(0,2)。
设直线AP2的解析式为:y=-![]() x+m,把A(0,2)代入得m=2。
x+m,把A(0,2)代入得m=2。
∴直线AP2的解析式为:y=-![]() x+2。
x+2。
由题意可得:![]() ,解得,
,解得,![]() 。∴P2(-
。∴P2(-![]() ,
,![]() )。
)。
∴P点坐标分别为P1(-![]() ,-
,-![]() )、P2(-
)、P2(-![]() ,
,![]() )。
)。


科目:初中数学 来源: 题型:
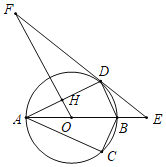
【题目】如图,在Rt△ABC中,∠ACB=90°,点O为△ABC外接圆的圆心,将△ABC沿AB翻折后得到△ABD.
(1)求证:点D在⊙O上;
(2)在直径AB的延长线上取一点E,使DE2=BEAE.
①求证:直线DE为⊙O的切线;
②过点O作OF∥BD交AD于点H,交ED的延长线于点F.若⊙O的半径为5,cos∠DBA=![]() ,求FH的长.
,求FH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司计划购进甲、乙两种规格的电脑,若购买甲种电脑3台,乙种电脑2台,共需资金23000元;若购买甲种电脑4台,乙种电脑3台,共需资金32000元.
(1)甲、乙两种电脑每台的价格分别是多少元;
(2)若公司计划购进这两种规格的电脑共20台,其中甲种电脑的数量不少于乙种电脑的数量,公司至多能够提供购买电脑的资金92000元,请设计几种购买方案供这个公司选择.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在以“关爱学生、安全第一”为主题的安全教育宣传月活动中,某学校为了了解本校学生的上学方式,在全校范围内随机抽查部分学生,了解到上学方式主要有:A:结伴步行、B:自行乘车、C:家人接送、D:其他方式,并将收集的数据整理绘制成如下两幅不完整的统计图.请根据图中信息,解答下列问题:
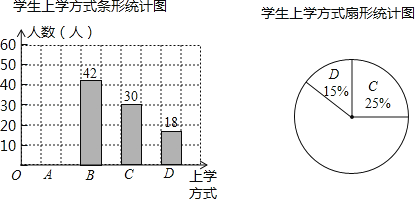
(1)本次抽查的学生人数是多少人?
(2)请补全条形统计图;请补全扇形统计图;
(3)“自行乘车”对应扇形的圆心角的度数是 度;
(4)如果该校学生有2000人,请你估计该校“家人接送”上学的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠ABC=72°.

(1)用直尺和圆规作∠ABC的平分线BD交AC于点D(保留作图痕迹,不要求写作法);
(2)在(1)中作出∠ABC的平分线BD后,求∠BDC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 为满足社区居民健身的需要,市政府准备采购若干套健身器材免费提供给社区,经考察,劲松公司有![]() 两种型号的健身器可供选择.
两种型号的健身器可供选择.
(1)劲松公司2015年每套![]() 型健身器的售价为
型健身器的售价为![]() 万元,经过连续两年降价,2017年每套售价为
万元,经过连续两年降价,2017年每套售价为![]() 万元,求每套
万元,求每套![]() 型健身器年平均下降率
型健身器年平均下降率![]() ;
;
(2)2017年市政府经过招标,决定年内采购并安装劲松公司![]() 两种型号的健身器材共
两种型号的健身器材共![]() 套,采购专项费总计不超过
套,采购专项费总计不超过![]() 万元,采购合同规定:每套
万元,采购合同规定:每套![]() 型健身器售价为
型健身器售价为![]() 万元,每套
万元,每套![]() 型健身器售价我
型健身器售价我![]() 万元.
万元.
①![]() 型健身器最多可购买多少套?
型健身器最多可购买多少套?
②安装完成后,若每套![]() 型和
型和![]() 型健身器一年的养护费分别是购买价的
型健身器一年的养护费分别是购买价的![]() 和
和![]() .市政府计划支出
.市政府计划支出![]() 万元进行养护.问该计划支出能否满足一年的养护需要?
万元进行养护.问该计划支出能否满足一年的养护需要?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步营造扫黑除恶专项斗争的浓厚宣传氛围,推进平安校园建设,甲、乙两所学校各租用一辆大巴车组织部分师生,分别从距目的地240千米和270千米的两地同时出发,前往“研学教育”基地开展扫黑除恶教育活动,已知乙校师生所乘大巴车的平均速度是甲校师生所乘大巴车的平均速度的1.5倍,甲校师生比乙校师生晚1小时到达目的地,分别求甲、乙两所学校师生所乘大巴车的平均速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com