
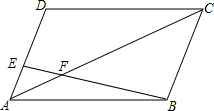
 如图,平行四边形ABCD中,AE:ED=1:2,S△AEF=6cm2,则S△CBF等于54cm2.
如图,平行四边形ABCD中,AE:ED=1:2,S△AEF=6cm2,则S△CBF等于54cm2. 分析 根据相似三角形的性质,可得△AEF∽△CBF,由已知可证$\frac{{S}_{△AEF}}{{S}_{△CBF}}$=($\frac{AE}{BC}$)2=$\frac{1}{9}$,继而求得S△CBF=9S△AEF=54cm2.
解答 解:∵AE:ED=1:2,
$\frac{AE}{AD}$=$\frac{1}{3}$,
∵AD∥BC,
∴△AEF∽△CBF,
∴$\frac{{S}_{△AEF}}{{S}_{△CBF}}$=($\frac{AE}{BC}$)2=$\frac{1}{9}$,
∴S△CBF=9S△AEF=54cm2.
故答案为:54cm2.
点评 此题主要考查了平行四边形的性质以及相似三角形的判定与性质等知识,得出△AEF∽△CBF是解题关键.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:选择题
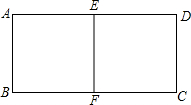 如图,把一个矩形纸片ABCD沿AD和BC的中点连线EF对折,要使矩形AEFB与原矩形相似,则原矩形长与宽的比为( )
如图,把一个矩形纸片ABCD沿AD和BC的中点连线EF对折,要使矩形AEFB与原矩形相似,则原矩形长与宽的比为( )| A. | 2:1 | B. | 3:1 | C. | $\sqrt{2}$:1 | D. | 4:1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
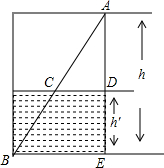 如图,一油桶高1m,桶内有油,一根木棒长1.2m,从桶盖的小口处斜插入桶内,一端插到桶底,另一端到小口,抽出木棒,量得棒上浸油部分长为0.48m,求桶内油面的高度.
如图,一油桶高1m,桶内有油,一根木棒长1.2m,从桶盖的小口处斜插入桶内,一端插到桶底,另一端到小口,抽出木棒,量得棒上浸油部分长为0.48m,求桶内油面的高度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
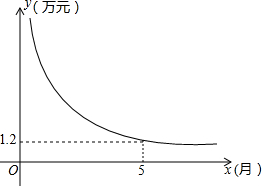 黄女士参加了上海通用汽车公司推出的分期付款购买汽车活动,她购买的别克汽车价格为16.3万元,交了首付之后每月付款y万元,x月结清余款,y与x的函数关系如图所示,试根据图象提供的信息回答下列问题.
黄女士参加了上海通用汽车公司推出的分期付款购买汽车活动,她购买的别克汽车价格为16.3万元,交了首付之后每月付款y万元,x月结清余款,y与x的函数关系如图所示,试根据图象提供的信息回答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
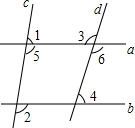 如图,∠1+∠2=180°,∠3=108°,求∠4的度数的过程填写完整.
如图,∠1+∠2=180°,∠3=108°,求∠4的度数的过程填写完整.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
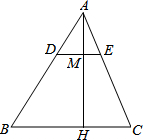 如图所示:AH是△ABC的边上的高,M为AH上一点,且AM:MH=1:2,过M引DE∥BC分别交AB,AC于点D,E,若BC=16cm、AH=9cm.
如图所示:AH是△ABC的边上的高,M为AH上一点,且AM:MH=1:2,过M引DE∥BC分别交AB,AC于点D,E,若BC=16cm、AH=9cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com