
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DO⊥AB,垂足为O,点B′在边AB上,且与点B关于直线DO对称,连接DB′,AD.
(1)求证:△DOB∽△ACB;
(2)若AD平分∠CAB,求线段BD的长;
(3)当△AB′D为等腰三角形时,求线段BD的长.
【答案】
(1)
证明:∵DO⊥AB,
∴∠DOB=∠DOA=90°,
∴∠DOB=∠ACB=90°,
又∵∠B=∠B,
∴△DOB∽△ACB;
(2)
解:∵∠ACB=90°,
∴AB=![]() =
=![]() =10,
=10,
∵AD平分∠CAB,DC⊥AC,DO⊥AB,
∴DC=DO,
在Rt△ACD和Rt△AOD中,
![]() ,
,
∴Rt△ACD≌Rt△AOD(HL),
∴AC=AO=6,
设BD=x,则DC=DO=8﹣x,OB=AB﹣AO=4,
在Rt△BOD中,根据勾股定理得:DO2+OB2=BD2,
即(8﹣x)2+42=x2,
解得:x=5,
∴BD的长为5;
(3)
解:∵点B′与点B关于直线DO对称,
∴∠B=∠OB′D,BO=B′O,BD=B′D,
∵∠B为锐角,
∴∠OB′D也为锐角,
∴∠AB′D为钝角,
∴当△AB′D为等腰三角形时,AB′=DB′,
∵△DOB∽△ACB,
∴![]() =
=![]() =
=![]() ,
,
设BD=5x,
则AB′=DB′=5x,BO=B′O=4x,
∵AB′+B′O+BO=AB,
∴5x+4x+4x=10,
解得:x=![]() ,
,
∴BD=![]() .
.
【解析】(1)由∠DOB=∠ACB=90°,∠B=∠B,容易证明△DOB∽△ACB;
(2)先由勾股定理求出AB,由角平分线的性质得出DC=DO,再由HL证明Rt△ACD≌Rt△AOD,得出AC=AO,设BD=x,则DC=DO=8﹣x,由勾股定理得出方程,解方程即可;
(3)根据题意得出当△AB′D为等腰三角形时,AB′=DB′,由△DOB∽△ACB,得出![]() ,设BD=5x,则AB′=DB′=5x,BO=B′O=4x,由AB′+B′O+BO=AB,得出方程,解方程求出x,即可得出BD.
,设BD=5x,则AB′=DB′=5x,BO=B′O=4x,由AB′+B′O+BO=AB,得出方程,解方程求出x,即可得出BD.
【考点精析】认真审题,首先需要了解相似图形(形状相同,大小不一定相同(放大或缩小);判定:①平行;②两角相等;③两边对应成比例,夹角相等;④三边对应成比例).


 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
【题目】一个不透明的盒子中有三张卡片,卡片上面分别标有字母a,b,c,每张卡片除字母不同外其他都相同,小玲先从盒子中随机抽出一张卡片,记下字母后放回并搅匀;再从盒子中随机抽出一张卡片并记下字母,用画树状图(或列表)的方法,求小玲两次抽出的卡片上的字母相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣![]() 经过点A(1,0)和点B(5,0),与y轴交于点C.
经过点A(1,0)和点B(5,0),与y轴交于点C.
(1)求此抛物线的解析式;
(2)以点A为圆心,作与直线BC相切的⊙A,求⊙A的半径
(3)在直线BC上方的抛物线上任取一点P,连接PB,PC,请问:△PBC的面积是否存在最大值?若存在,求出这个最大值的此时点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若两个扇形满足弧长的比等于它们半径的比,则这称这两个扇形相似.如图,如果扇形AOB与扇形A101B1是相似扇形,且半径OA:O1A1=k(k为不等于0的常数).那么下面四个结论:①∠AOB=∠A101B1;②△AOB∽△A101B1;③![]() =k;④扇形AOB与扇形A101B1的面积之比为k2 . 成立的个数为( )
=k;④扇形AOB与扇形A101B1的面积之比为k2 . 成立的个数为( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在菱形ABCD中,E是CD上的一点,连接BE交AC于O,连接DO并延长交BC于E.
(1)求证:△FOC≌△EOC;
(2)将此图中的AD、BE分别延长交于点N,作EM∥BC交CN于M,再连接FM即得到图2.
求证:①![]() ;②FD=FM.
;②FD=FM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年,我省启动了“关爱留守儿童工程”.某村小为了了解各年级留守儿童的数量,对一到六年级留守儿童数量进行了统计,得到每个年级的留守儿童人数分别为10,15,10,17,18,20.对于这组数据,下列说法错误的是( )
A.平均数是15
B.众数是10
C.中位数是17
D.方差是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装公司招工广告承诺:熟练工人每月工资至少3000元.每天工作8小时,一个月工作25天.月工资底薪800元,另加计件工资.加工1件A型服装计酬16元,加工1件B型服装计酬12元.在工作中发现一名熟练工加工1件A型服装和2件B型服装需4小时,加工3件A型服装和1件B型服装需7小时.(工人月工资=底薪+计件工资)
(1)一名熟练工加工1件A型服装和1件B型服装各需要多少小时?
(2)一段时间后,公司规定:“每名工人每月必须加工A,B两种型号的服装,且加工A型服装数量不少于B型服装的一半”.设一名熟练工人每月加工A型服装a件,工资总额为W元.请你运用所学知识判断该公司在执行规定后是否违背了广告承诺?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=13cm,AC=12cm,BC=5cm.D是BC边上的一个动点,连接AD,过点C作CE⊥AD于E,连接BE,在点D变化的过程中,线段BE的最小值是cm. 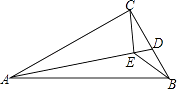
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com