
【题目】如图1,在△ABC中,AB=BC=5,AC=6,△ECD是△ABC沿BC方向平移得到的,连接AE、BE,且AC和BE相交于点O.
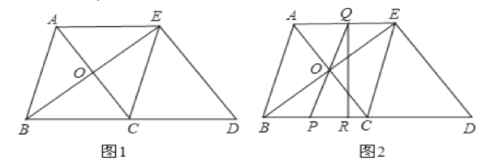
(1)求证:四边形ABCE是菱形;
(2)如图2,P是线段BC上一动点(不与B. C重合),连接PO并延长交线段AE于点Q,过Q作QR⊥BD交BD于R.
①四边形PQED的面积是否为定值?若是,请求出其值;若不是,请说明理由;
②以点P、Q、R为顶点的三角形与以点B. C. O为顶点的三角形是否可能相似?若可能,请求出线段BP的长;若不可能,请说明理由.
【答案】(1)见解析;(2)①24,②![]() ;
;
【解析】
(1)利用平移的性质以及菱形的判定得出即可;
(2)①首先过E作EF⊥BD交BD于F,则∠EFB=90°,证出△QOE≌△POB,利用QE=BP,得出四边形PQED的面积为定值;
②当∠QPR=∠BCO时,△PQR∽△CBO,此时有OP=OC=3,过O作OG⊥BC交BC于G,得出△OGC∽△BOC,利用相似三角形的性质得出CG的长,进而得出BP的长.
(1)证明:∵△ABC沿BC方向平移得到△ECD,
∴EC=AB,AE=BC,
∵AB=BC,
∴EC=AB=BC=AE,
∴四边形ABCE是菱形;
(2)①四边形PQED的面积是定值,理由如下:
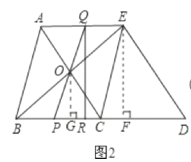
过E作EF⊥BD交BD于F,则∠EFB=90°,
∵四边形ABCE是菱形,
∴AE∥BC,OB=OE,OA=OC,OC⊥OB,
∵AC=6,
∴OC=3,
∵BC=5,
∴OB=4,sin∠OBC=![]() ,
,
∴BE=8,
∴EF=BEsin∠OBC=8×![]() ,
,
∵AE∥BC,
∴∠AEO=∠CBO,四边形PQED是梯形,
在△QOE和△POB中
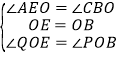 ,
,
∴△QOE≌△POB,
∴QE=BP,
∴S![]() =
=![]() (QE+PD)×EF=
(QE+PD)×EF=![]() (BP+DP)×EF=
(BP+DP)×EF=![]() ×BD×EF=
×BD×EF=![]() ×2BC×EF=BC×EF=5×
×2BC×EF=BC×EF=5×![]() =24;
=24;
②△PQR与△CBO可能相似,
∵∠PRQ=∠COB=90°,∠QPR>∠CBO,
∴当∠QPR=∠BCO时,△PQR∽△CBO,此时有OP=OC=3.
过O作OG⊥BC交BC于G.
∵∠OCB=∠OCB,∠OGC=∠BOC,
∴△OGC∽△BOC,
∴CG:CO=CO:BC,
即CG:3=3:5,
∴CG=![]() ,
,
∴BP=BCPC=BC2CG=52×![]() =
=![]() .
.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】某商场在“双十一”促销活动中决定对购买空调的顾客实行现金返利.规定每购买一台空调,商场返利若干元.经调查,销售空调数量y1(单位:台)与返利x(单位:元)之间的函数表达式为![]() .每台空调的利润y2(单位:元)与返利x的函数图像如图所示.
.每台空调的利润y2(单位:元)与返利x的函数图像如图所示.
(1)求y2与x之间的函数表达式;

(2)每台空调返利多少元才能使销售空调的总利润最大?最大总利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() .
.
(1)![]() 为何值时,
为何值时,![]() 随
随![]() 的增大而减小?
的增大而减小?
(2)![]() 为何值时,函数图象与
为何值时,函数图象与![]() 轴的交点在
轴的交点在![]() 轴下方?
轴下方?
(3)![]() ,
,![]() 分别是何值时,函数图象经过原点?
分别是何值时,函数图象经过原点?
(4)当![]() ,
,![]() 时,求这个一次函数的图象与两个坐标轴的交点.
时,求这个一次函数的图象与两个坐标轴的交点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自实施新教育改革后,学生的自主学习、合作交流能力有很大提高,张老师为了了解所教班级学生自主学习、合作交流的具体情况,对本班部分同学进行了为期半个月的跟踪调查,并将调查结果分为四类:A.特别好;B.好;C.一般;D.较差,并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
(1)本次调查中,张老师一共调查了多少名同学?
(2)求出调查中C类女生及D类男生的人数,将条形统计图补充完整;
(3)为了共同进步,张老师想从被调查的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把四张形状大小完全相同的小长方形卡片(如图①)不重叠的放在一个长为![]() ,宽为
,宽为![]() 的长方形内,该长方形内部未被卡片覆盖的部分用阴影表示.
的长方形内,该长方形内部未被卡片覆盖的部分用阴影表示.

(1)能否用只含![]() 的式子表示出图②中两块阴影部分的周长和?_____(填“能”或“不能”);(2)若能,请你用只含
的式子表示出图②中两块阴影部分的周长和?_____(填“能”或“不能”);(2)若能,请你用只含![]() 的式子表示出中两块阴影部分的周长和;若不能,请说明理由_____.
的式子表示出中两块阴影部分的周长和;若不能,请说明理由_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:①abc>0;②b2=4ac;③4a+2b+c>0;④3a+c>0,其中正确的结论是________.(写出正确命题的序号)
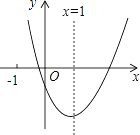
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一副三角板按如图1方式拼接在一起,其中边OA、OC与直线EF重合,![]() ,
,![]()
![]() 图1中
图1中![]() ______
______![]()
![]() 如图2,三角板COD固定不动,将三角板AOB绕着点O按顺时针方向旋转一个角度
如图2,三角板COD固定不动,将三角板AOB绕着点O按顺时针方向旋转一个角度![]() ,在转动过程中两块三角板都在直线EF的上方:
,在转动过程中两块三角板都在直线EF的上方:
![]() 当OB平分OA、OC、OD其中的两边组成的角时,求满足要求的所有旋转角度
当OB平分OA、OC、OD其中的两边组成的角时,求满足要求的所有旋转角度![]() 的值;
的值;
![]() 是否存在
是否存在![]() ?若存在,求此时的
?若存在,求此时的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励居民节约用电,某市采用价格调控手段达到省电目的.该市电费收费标准如下表(按月结算) :
每月用电量/度 | 电价/(元/度) |
不超过 |
|
超过 |
|
超过 |
|
解答下列问题:
(1)某居民![]() 月份用电量为
月份用电量为![]() 度,请问该居民
度,请问该居民![]() 月应缴电费多少元?
月应缴电费多少元?
(2)设某月的用电量为![]() 度
度![]() ,试写出不同用电量范围应缴的电费(用
,试写出不同用电量范围应缴的电费(用![]() 表示) .
表示) .
(3)某居民![]() 月份缴电费
月份缴电费![]() 元,求该居民
元,求该居民![]() 月份的用电量.
月份的用电量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
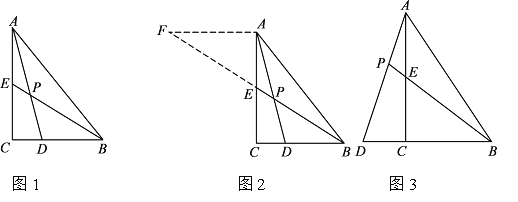
小昊遇到这样一个问题:如图1,在△ABC中,∠ACB=90°,BE是AC边上的中线,点D在BC边上,CD:BD=1:2,AD与BE相交于点P,求![]() 的值.
的值.
小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).请回答:![]() 的值为 .
的值为 .
参考小昊思考问题的方法,解决问题:
如图 3,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC:AC=1:2:3 .
(1)求![]() 的值;
的值;
(2)若CD=2,则BP=__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com