
【题目】如图,![]() ,
,![]() ,
,![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
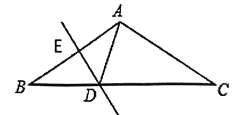
(1)求![]() 的度数;
的度数;
(2)求证:![]() .
.
【答案】(1)60°;(2)见解析.
【解析】
(1)先根据等腰三角形的性质可求出∠B=∠C=30°,再由垂直平分线的性质可得AD=BD,所以∠DAB=∠B =30°,又因为![]() ,所以∠CAD=90°,再根据三角形的内角和定理可求出结果;
,所以∠CAD=90°,再根据三角形的内角和定理可求出结果;
(2)先根据垂直平分线的性质可得到AD=BD,在直角三角形ACD中,根据30°角所对的直角边等于斜边的一半,可得到CD=2AD,再等量代换即可得到结论.
(1)解:∵![]() ,
,![]() ,
,
∴∠B=∠C=30°,
∵![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,
,
∴AD=BD,
∴∠DAB=∠B =30°,
∴∠CAD=90°.
∵∠CAD+∠ADC+∠C=180°
∴∠ADC=180°-∠CAD-∠C
=180°-90°-30°
=60°.
答:![]() 的度数60°;
的度数60°;
(2)证明:由(1)可得AD=BD,△ACD是直角三角形.
在Rt△ACD中,
∵∠C=30°,
∴CD=2AD.
∵AD=BD,
∴CD=2BD.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点![]() 的直线
的直线![]() 与直线
与直线![]() 相交于点
相交于点![]() .
.
(1)直线![]() 的关系式为 ;直线
的关系式为 ;直线![]() 的关系式为 (直接写出答案,不必写过程).
的关系式为 (直接写出答案,不必写过程).
(2)求![]() 的面积.
的面积.
(3)若有一动点![]() 沿路线
沿路线![]() 运动,当
运动,当![]() 时,求点
时,求点![]() 坐标.
坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中,横坐标为a的点A在反比例函数y1═![]() (x>0)的图象上,点A′与点A关于点O对称,一次函数y2=mx+n的图象经过点A′.
(x>0)的图象上,点A′与点A关于点O对称,一次函数y2=mx+n的图象经过点A′.
(1)设a=2,点B(4,2)在函数y1、y2的图象上.
①分别求函数y1、y2的表达式;
②直接写出使y1>y2>0成立的x的范围;
(2)如图①,设函数y1、y2的图象相交于点B,点B的横坐标为3a,△AA'B的面积为16,求k的值;
(3)设m=![]() ,如图②,过点A作AD⊥x轴,与函数y2的图象相交于点D,以AD为一边向右侧作正方形ADEF,试说明函数y2的图象与线段EF的交点P一定在函数y1的图象上.
,如图②,过点A作AD⊥x轴,与函数y2的图象相交于点D,以AD为一边向右侧作正方形ADEF,试说明函数y2的图象与线段EF的交点P一定在函数y1的图象上.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)的长方形ABCD中,E点在AD上,且BE=2AE.今分别以BE、CE为折线,将A、D向BC的方向折过去,图(2)为对折后A、B、C、D、E五点均在同一平面上的位置图.若图(2)中,∠AED=15°,则∠BCE的度数为_____.
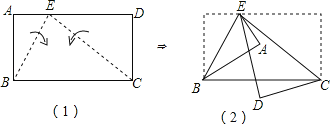
查看答案和解析>>
科目:初中数学 来源: 题型:
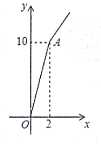
【题目】某玉米种子的价格为![]() 元/千克,如果一次购买2千克以上的种子,超过2千克部分的种子价格打8折,某科技人员对付款金额和购买量这两个变量的对应关系用列表法做了分析,并绘制出了函数图象,以下是该科技人员绘制的图象和表格的不完整资料,已知点A的坐标为
元/千克,如果一次购买2千克以上的种子,超过2千克部分的种子价格打8折,某科技人员对付款金额和购买量这两个变量的对应关系用列表法做了分析,并绘制出了函数图象,以下是该科技人员绘制的图象和表格的不完整资料,已知点A的坐标为![]() ,请你结合表格和图象:
,请你结合表格和图象:
付款金额 |
| 7.5 | 10 | 12 |
|
购买量 | 1 | 1.5 | 2 | 2.5 | 3 |
(1)![]() ,
,![]() ;
;
(2)求出当![]() 时,
时,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,D是线段BC的延长线上一点,以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.
(1)如图1,点D在线段BC的延长线上移动,若∠BAC=30°,则∠DCE= .
(2)设∠BAC=α,∠DCE=β:
①如图1,当点D在线段BC的延长线上移动时,α与β之间有什么数量关系?请说明理由;
②当点D在直线BC上(不与B、C重合)移动时,α与β之间有什么数量关系?请直接写出你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象分别交
的图象分别交![]() 轴、
轴、![]() 轴于点
轴于点![]() 、点
、点![]() ,与反比例函数
,与反比例函数![]() 的图象在第四象限的相交于点
的图象在第四象限的相交于点![]() ,并且
,并且![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,已知
,已知![]() ,且
,且![]()
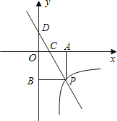
![]() 求上述一次函数与反比例函数的表达式;
求上述一次函数与反比例函数的表达式;
![]() 求一次函数与反比例函数的另一个交点坐标.
求一次函数与反比例函数的另一个交点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=2,AC=3,1<BC<5,分别以AB、BC、AC为边向外作正方形ABIH、BCDE和正方形ACFG,则图中阴影部分的最大面积为( )
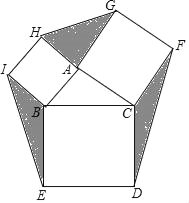
A. 6 B. 9 C. 11 D. 无法计算
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com