
 在如图的坐标平面上,有一条通过点P(-3,-2)的直线y=-x+b,该直线分别于x轴、y轴相交于点A,B,则PA:PB的值为( )
在如图的坐标平面上,有一条通过点P(-3,-2)的直线y=-x+b,该直线分别于x轴、y轴相交于点A,B,则PA:PB的值为( )A、
| ||
B、
| ||
C、
| ||
D、
|
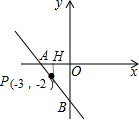 解:把P(-3,-2)代入y=-x+b得3+b=-2,解得b=-5,
解:把P(-3,-2)代入y=-x+b得3+b=-2,解得b=-5,| b |
| k |


科目:初中数学 来源: 题型:
 我海军某舰队为了提升实战能力,进行夺岛演练.如图,位于A处的甲舰沿北偏东50°的方向以每小时40海里的速度向岛屿P出发,同时在A处正东方向的B处有乙舰从B处沿西北方向出发,2小时后两舰同时到达岛屿P处,问乙舰每小时航行多少海里?(sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,
我海军某舰队为了提升实战能力,进行夺岛演练.如图,位于A处的甲舰沿北偏东50°的方向以每小时40海里的速度向岛屿P出发,同时在A处正东方向的B处有乙舰从B处沿西北方向出发,2小时后两舰同时到达岛屿P处,问乙舰每小时航行多少海里?(sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com