
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
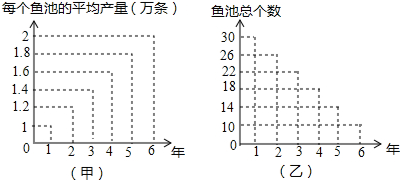
分析 根据折线统计图所给出的数据,计算出各年份的产鱼量,再分别对每一项进行分析即可得出答案.
解答 解:根据题意得:
①该地第3年养鱼池产鱼数量为1.4×22=30.8万条,故本选项错误;
②该地第2年养鱼池产鱼的数量是1.2×26=31.2万条,第3年养鱼池产鱼的数量是1.4×22=30.8万条,则该地第2年养鱼池产鱼的数量高于第3年养鱼池产鱼的数量,故本选项错误;
③该地第1年养鱼池产鱼数量为1×30=30万条,第2年养鱼池产鱼数量为1.2×22=31.2万条,则该地这6年养鱼池产鱼的数量逐年减少是错误的;
④这6年中,第6年该地养鱼池产鱼的数量是2×10=20万条,最少,正确;
故选C.
点评 此题考查了折线统计图,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键,折线统计图表示的是事物的变化情况.


科目:初中数学 来源: 题型:选择题
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
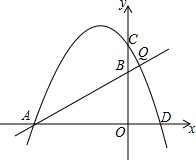 设直线y=$\frac{1}{2}$x+2与抛物线y=-$\frac{1}{2}$x2-x+4交于点A,点Q,若在x轴上方的抛物线上只存在相异的两点M、N,S△MAQ=S△NAQ=S,则S的取值范围$\frac{15}{2}$<S<$\frac{125}{16}$.
设直线y=$\frac{1}{2}$x+2与抛物线y=-$\frac{1}{2}$x2-x+4交于点A,点Q,若在x轴上方的抛物线上只存在相异的两点M、N,S△MAQ=S△NAQ=S,则S的取值范围$\frac{15}{2}$<S<$\frac{125}{16}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ($\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$) | B. | (-$\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$) | C. | (-$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$) | D. | ($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com