练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，△PAB与△PCD均为等腰直角三角形，点C在PB上，若△ABC与△BCD的面积之和为10，则△PAB与△PCD的面积之差为（　　）

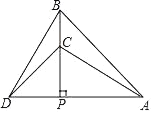
    A. 5B. 10C. l5D. 20

    【答案】B

    【解析】

    由题意得，S△ABC+S△BCD＝BCPA+BCPD＝BC(PA+PD)＝10，要求△PAB与△PCD的面积之差，即PA2﹣PB2＝ (PA+PD)(PA﹣PD)＝ (PB﹣PC)(PA+PD)＝BC(PA+PD)，即可求解.

    解：依题意，

    ∵△PAB与△PCD均为等腰直角三角形

    ∴PB＝PB，PC＝PD

    ∴S△PAB﹣S△PCD＝PA2﹣PD2

    ＝(PA+PD)(PA﹣PD)

    ＝(PB﹣PC)(PA+PD)

    ＝BC(PA+PD)，

    又∵S△ABC+S△BCD＝BCPA+BCPD＝BC(PA+PD)＝10

    ∴S△PAB﹣S△PCD＝10．

    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

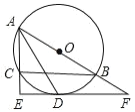
    【题目】如图， O 是 ABC 的外接圆，AB 为直径，∠BAC 的平分线交O 于点 D，过点 D 作 DE⊥AC 分别交 AC、AB 的延长线于点 E、F．

    （1）求证：EF 是O 的切线；

    （2）若 AC=6，CE=3，求弧BD 的长度．（结果保留π）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“每天锻炼一小时，健康生活一辈子”．为了选拔“阳光大课间”领操员，学校组织初中三个年级推选出来的15名领操员进行比赛，成绩如下表：

    成绩/分

    7

    8

    9

    10

    人数/人

    2

    5

    4

    4

    （1）这组数据的众数是多少，中位数是多少．

    （2）已知获得2018年四川省南充市的选手中，七、八、九年级分别有1人、2人、1人，学校准备从中随机抽取两人领操，求恰好抽到八年级两名领操员的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】市化工材料经销公司购进一种化工原料若干千克，价格为每千克30元．物价部门规定其销售单价不高于每千克60元，不低于每千克30元．经市场调查发现：日销售量（千克）是销售单价（元）的一次函数，且当=40时，=120；=50时，=100．在销售过程中，每天还要支付其他费用500元．

    （1）求出与的函数关系式，并写出自变量的取值范围．

    （2）求该公司销售该原料日获利（元）与销售单价（元）之间的函数关系式．

    （3）当销售单价为多少元时，该公司日获利最大？最大获利是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB是⊙O的直径，射线BC交⊙O于点D，E是劣弧AD上一点，且，过点E作EF⊥BC于点F，延长FE和BA的延长线交与点G．

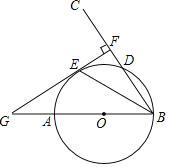
    （1）证明：GF是⊙O的切线；

    （2）若AG＝6，GE＝6，求△GOE的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】图1是安装在倾斜屋顶上的热水器，图2是安装热水器的侧面示意图．已知屋面AE的倾斜角∠EAD为22°，长为2米的真空管AB与水平线AD的夹角为37°，安装热水器的铁架竖直管CE的长度为0.5米．

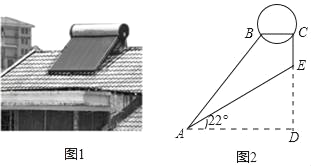
    (1)真空管上端B到水平线AD的距离．

    (2)求安装热水器的铁架水平横管BC的长度(结果精确到0.1米)

    参考数据：sin37°≈，cos37°≈，tan37°≈，sin22°≈，cos22°≈，tan22°≈

    查看答案和解析>>

    科目：初中数学 来源： 题型：

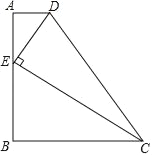
    【题目】如图，在四边形ABCD中，AD∥BC，AB⊥BC，点E在AB上，∠DEC＝90°．

    （1）求证：△ADE∽△BEC．

    （2）若AD＝1，BC＝3，AE＝2，求AB的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

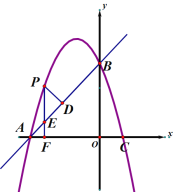
    【题目】如图，在平面直角坐标系xOy中，抛物线y=ax2+bx+c经过A、B、C三点，已知点A（﹣3，0），B（0，3），C（1，0）．

    （1）求此抛物线的解析式;

    （2）点P是直线AB上方的抛物线上一动点，（不与点A、B重合），过点P作x轴的垂线，垂足为F，交直线AB于点E，作PD⊥AB于点D．动点P在什么位置时，△PDE的周长最大，求出此时P点的坐标；

    （3）在直线上是否存在点M，使得∠MAC=2∠MCA，若存在，求出M点坐标.若不存在，说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，PA，PB是⊙O的切线，A，B是切点，点C是劣弧AB上的一点，若∠P＝40°，则∠ACB等于(　　)

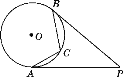
    A. 80° B. 110° C. 120° D. 140°

    查看答案和解析>>

    同步练习册答案