
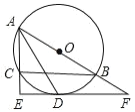
【题目】如图, O 是 ABC 的外接圆,AB 为直径,∠BAC 的平分线交O 于点 D,过点 D 作 DE⊥AC 分别交 AC、AB 的延长线于点 E、F.
(1)求证:EF 是O 的切线;
(2)若 AC=6,CE=3,求弧BD 的长度.(结果保留π)
科目:初中数学 来源: 题型:
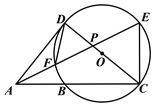
【题目】如图,△ACE,△ACD均为直角三角形,∠ACE=90°,∠ADC=90°,AE与CD相交于点P,以CD为直径的⊙O恰好经过点E,并与AC,AE分别交于点B和点F.
(1)求证:∠ADF=∠EAC.
(2)若PC=![]() PA,PF=1,求AF的长.
PA,PF=1,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A、B是⊙O上两点,△OAB外角的平分线交⊙O于另一点C,CD⊥AB交AB的延长线于D.
(1)求证:CD是⊙O的切线;
(2)E为![]() 的中点,F为⊙O上一点,EF交AB于G,若tan∠AFE=
的中点,F为⊙O上一点,EF交AB于G,若tan∠AFE=![]() ,BE=BG,EG=3
,BE=BG,EG=3![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是
A.一个游戏中奖的概率是![]() ,则做100次这样的游戏一定会中奖
,则做100次这样的游戏一定会中奖
B.为了了解全国中学生的心理健康状况,应采用普查的方式
C.一组数据0,1,2,1,1的众数和中位数都是1
D.若甲组数据的方差![]() ,乙组数据的方差
,乙组数据的方差![]() ,则乙组数据比甲组数据稳定
,则乙组数据比甲组数据稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
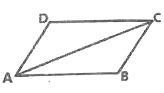
【题目】如图,已知平行四边形![]() ,
,![]() 是对角线.
是对角线.
(1)求作线段![]() 的垂直平分线,交
的垂直平分线,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .(要求尺规作图,不写作法,保留作图痕迹)
.(要求尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,连接![]() ,求证:四边形AFCE是菱形.
,求证:四边形AFCE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
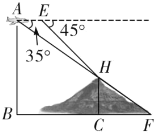
【题目】如图所示,为了测量某矿山CH的高度,科考组在距离矿山一段距离的B点乘坐直升机垂直上升2000米至A点,在A点,在A点观察H点的俯角为![]() ,然后乘坐直升机从A水平向前飞行500米到E点,此时观察H点的俯角为
,然后乘坐直升机从A水平向前飞行500米到E点,此时观察H点的俯角为![]() ,所有的点都在同一平面内,科考队至此完成了数据监测,请你依据数据计算科考队测得的矿山高度.(结果保留整数,参考数据:
,所有的点都在同一平面内,科考队至此完成了数据监测,请你依据数据计算科考队测得的矿山高度.(结果保留整数,参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
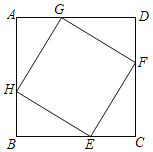
【题目】如图,点E,F,G,H分别位于边长为a的正方形ABCD的四条边上,四边形EFGH也是正方形,AG=x,正方形EFGH的面积为y.
(1)当a=2,y=3时,求x的值;
(2)当x为何值时,y的值最小?最小值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△PAB与△PCD均为等腰直角三角形,点C在PB上,若△ABC与△BCD的面积之和为10,则△PAB与△PCD的面积之差为( )
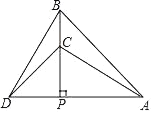
A. 5B. 10C. l5D. 20
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com