
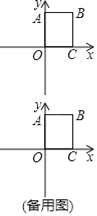
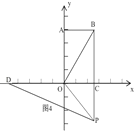
【题目】如图,在平面直角坐标系中,四边形OABC为矩形,点A(0,8),C(6,0).动点P从点B出发,以每秒1个单位长的速度沿射线BC方向匀速运动,设运动时间为t秒.
(1)当t= s时,以OB、OP为邻边的平行四边形是菱形;
(2)当点P在OB的垂直平分线上时,求t的值;
(3)将△OBP沿直线OP翻折,使点B的对应点D恰好落在x轴上,求t的值.
【答案】(1)16;(2)t=![]() ;(3)满足条件的t的值为5s或20s.
;(3)满足条件的t的值为5s或20s.
【解析】试题分析:(1)先有菱形的性质得出PC=BC=8,进而得出BP=16即可得出结论;
(2)由线段的垂直平分线的性质得出PO=PB=t,再利用勾股定理即可求出结论;
(3)分点P在x轴坐标轴和负半轴上,利用勾股定理即可建立方程求解.
试题解析:(1)如图1,
∵A(0,8),∴OA=8,C(6,0),∴OC=6,
∵四边形OABC是矩形,∴BC=OA=8,
∵以OB、OP为邻边的平行四边形是菱形,∴CP=BC=OA=8,
∴BP=BC+CP=16,t=16÷1=16s,
故答案为16;
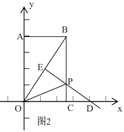
(2)如图2,∵点P是OB的垂直平分线上,∴PO=PB=t,∴PC=BC﹣PB=8﹣t,
在Rt△POC中,OC=6,根据勾股定理得,OC2+PC2=OP2,∴62+(8﹣t)2=t2,
∴t=![]() ;
;
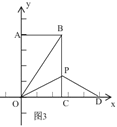
(3)当点P在x轴的坐标轴上时,如图3,
由折叠知,△OBP≌△ODP,∴PD=PB=t,OD=OB=![]() =10,∴CD=OD﹣OC=4,
=10,∴CD=OD﹣OC=4,
在Rt△PCD中,CD=4,PC=BC﹣PB=8﹣t,PD=t,
根据勾股定理得,PC2+CD2=PD2,∴42+(8﹣t)2=t2,∴t=5,
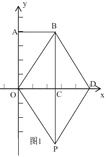
当点P在x轴负半轴上时,如图4,
由折叠知,PB=PD=t,OD=OB=10,∴CD=OD+OC=16,PC=t﹣8,
在Rt△PCD中,根据勾股定理得,PC2+CD2=PD2,∴(t﹣8)2+162=t2,∴t=20,
即:满足条件的t的值为5s或20s.


科目:初中数学 来源: 题型:
【题目】如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )

A. ∠M=∠N B. AM=CN C. AB=CD D. AM∥CN
查看答案和解析>>
科目:初中数学 来源: 题型:
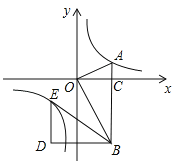
【题目】如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A(![]() ,1)在反比例函数
,1)在反比例函数![]() 的图象上.
的图象上.
(1)求反比例函数![]() 的表达式;
的表达式;
(2)在x轴的负半轴上存在一点P,使得S△AOP=![]() S△AOB,求点P的坐标;
S△AOB,求点P的坐标;
(3)若将△BOA绕点B按逆时针方向旋转60°得到△BDE.直接写出点E的坐标,并判断点E是否在该反比例函数的图象上,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
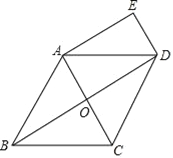
【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形;
(2)若AB=2![]() ,AC=2,求四边形AODE的周长.
,AC=2,求四边形AODE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)请分别写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(2)小明选择哪家快递公司更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学发现自己一本书的宽与长之比是黄金比约为0.618.已知这本书的长为20cm,则它的宽约为( )
A.12.36cmB.13.6cmC.32.386cmD.7.64cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com