
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,直线
两点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .点
.点![]() 是抛物线上一动点,过点
是抛物线上一动点,过点![]() 作直线
作直线![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() .
.

![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 若点
若点![]() 在
在![]() 轴上方的抛物线上,当
轴上方的抛物线上,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
![]() 若点
若点![]() ’是点
’是点![]() 关于直线
关于直线![]() 的对称点,当点
的对称点,当点![]() ’落在
’落在![]() 轴上时,请直接写出
轴上时,请直接写出![]() 的值.
的值.
【答案】(1)抛物线的解析式为![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() 或
或![]() 存在满足条件的
存在满足条件的![]() 的值为
的值为![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)将抛物线与![]() 的轴交点
的轴交点![]() 、
、![]() 代入解析式
代入解析式![]() ,即可得出结论.(2)由题可知,P,E,F三点的横坐标均为m,用含m的代数式分别表示PE、EF,根据
,即可得出结论.(2)由题可知,P,E,F三点的横坐标均为m,用含m的代数式分别表示PE、EF,根据![]() 列出方程即可得出结论.(3)根据
列出方程即可得出结论.(3)根据![]() ’是点
’是点![]() 关于直线
关于直线![]() 的对称点证明
的对称点证明![]() 为菱形,根据PE=CE,用含m的代数式列方程求解;当P点位于y轴上时,四边形
为菱形,根据PE=CE,用含m的代数式列方程求解;当P点位于y轴上时,四边形![]() 不存在,根据抛物线的性质即可得到m的值.
不存在,根据抛物线的性质即可得到m的值.
解:![]() ∵抛物线
∵抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,
两点,
∴![]() ,
,
解得![]() ,
,
∴抛物线的解析式为![]() .
.
![]() ∵点
∵点![]() 的横坐标为
的横坐标为![]() ,
,
∴![]() ,
,![]() ,
,![]() .
.
∴![]() ,
,
![]() .
.
由题意,![]() ,即:
,即:![]()
①若![]() ,整理得:
,整理得:![]() ,
,
解得:![]() 或
或![]() ;
;
②若![]() ,整理得:
,整理得:![]() ,
,
解得:![]() 或
或![]() .
.
由题意,![]() 的取值范围为:
的取值范围为:![]() ,故
,故![]() 、
、![]() 这两个解均舍去.
这两个解均舍去.
∴![]() 或
或![]() .
.
∴点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
![]() 假设存在.
假设存在.
作出示意图如下:

∵点![]() 、
、![]() 关于直线
关于直线![]() 对称,
对称,
∴![]() ,
,![]() ,
,![]() .
.
∵![]() 平行于
平行于![]() 轴,∴
轴,∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,即四边形
,即四边形![]() 是菱形.
是菱形.
当四边形![]() 是菱形存在时,
是菱形存在时,
由直线![]() 解析式
解析式![]() ,可得
,可得![]() ,
,![]() ,由勾股定理得
,由勾股定理得![]() .
.
过点![]() 作
作![]() 轴,交
轴,交![]() 轴于点
轴于点![]() ,易得
,易得![]() ,
,
∴![]() ,即
,即![]() ,解得
,解得![]() ,
,
∴![]() ,又由
,又由![]() 可知:
可知:![]()
∴![]() .
.
①若![]() ,整理得:
,整理得:![]() ,解得
,解得![]() 或
或![]() ;
;
②若![]() ,整理得:
,整理得:![]() ,解得
,解得![]() ,
,![]() .
.
由题意,![]() 的取值范围为:
的取值范围为:![]() ,故
,故![]() 这个解舍去.
这个解舍去.
当四边形![]() 是菱形这一条件不存在时,
是菱形这一条件不存在时,
此时![]() 点横坐标为
点横坐标为![]() ,
,![]() ,
,![]() ,
,![]() 三点重合与
三点重合与![]() 轴上,也符合题意,
轴上,也符合题意,
∴![]()
综上所述,存在满足条件的![]() 的值为
的值为![]() 或
或![]() 或
或![]() 或
或![]() .
.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】如图所示,在矩形ABCD中,AD=4,点E在边AD上,连接CE,以CE为边向右上方作正方形CEFG,作FH⊥AD,且垂足H在边AD上,连接AF.
(1)求证:FH=ED;
(2)设AE=x,是否存在某个x的值,使得△AEF的面积为3?若存在,求出x的值,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大拇指与小拇指尽量张开时,两指尖的距离称为指距.人体构造学的研究成果表明,一般情况下人的指距d和身高h成如下所示的关系.

指距d(cm) | 20 | 21 | 22 | 23 |
身高h(cm) | 160 | 169 | 178 | 187 |
(1)直接写出身高h与指距d的函数关系式;
(2)姚明的身高是226厘米,可预测他的指距约为多少?(精确到0.1厘米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分9分)
根据要求,解答下列问题.
(1)根据要求,解答下列问题.
①方程x2-2x+1=0的解为________________________;
②方程x2-3x+2=0的解为________________________;
③方程x2-4x+3=0的解为________________________;
…… ……
(2)根据以上方程特征及其解的特征,请猜想:
①方程x2-9x+8=0的解为________________________;
②关于x的方程________________________的解为x1=1,x2=n.
(3)请用配方法解方程x2-9x+8=0,以验证猜想结论的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓是单价为40元,设第二个月单价降低![]() 元.
元.
(1)填表:(不需化简)

(2)如果批发商希望通过销售这批T恤获利9000元,那么第二个月的单价应是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三个登山爱好者经常相约去登山,今年1月甲参加了两次登山活动.
(1)1月1日甲与乙同时开始攀登一座900米高的山,甲的平均攀登速度是乙的1.2倍,结果甲比乙早15分钟到达顶峰.求甲的平均攀登速度是每分钟多少米?
(2)1月6日甲与丙去攀登另一座h米高的山,甲保持第(1)问中的速度不变,比丙晚出发0.5小时,结果两人同时到达顶峰,问甲的平均攀登速度是丙的多少倍?(用含h的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
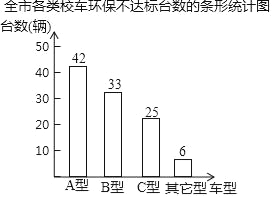
【题目】长春市对全市各类(A型、B型、C型.其它型)校车共848辆进行环保达标普查,普查结果绘制成如下条形统计图:
(1)求全市各类环保不达标校车的总数;
(2)求全市848辆校车中环保不达标校车的百分比;
(3)规定环保不达标校车必须进行维修,费用为:A型500元/辆,B型1000元/辆,C型600元/辆,其它型300元/辆,求全市需要进行维修的环保不达标校车维修费的总和;
(4)若每辆校车乘坐40名学生,那么一次性维修全部不达标校车将会影响全市80000名学生乘校车上学的百分比是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为改善南宁市的交通现状,市政府决定修建地铁,甲、乙两工程队承包地铁1号线的某段修建工作,从投标书中得知:甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的3倍;若由甲队先做20天,剩下的工程再由甲、乙两队合作10天完成.
![]() 求甲、乙两队单独完成这项工程各需多少天?
求甲、乙两队单独完成这项工程各需多少天?
![]() 已知甲队每天的施工费用为
已知甲队每天的施工费用为![]() 万元,乙队每天的施工费用为
万元,乙队每天的施工费用为![]() 万元,工程预算的施工费用为500万元,为缩短工期,拟安排甲、乙两队同时开工合作完成这项工程,那么工程预算的施工费用是否够用?若不够用,需增加多少万元?
万元,工程预算的施工费用为500万元,为缩短工期,拟安排甲、乙两队同时开工合作完成这项工程,那么工程预算的施工费用是否够用?若不够用,需增加多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com