
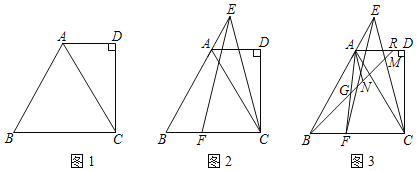
【题目】已知四边形ABCD中,AD∥BC,∠D=90°,AC平分∠BAD,∠ACD=30°
(1)如图1,求证:△ABC是等边三角形;
(2)如图2,点E在边BA的延长线上,在边BC上取一点F,连接EC、EF且EC=EF,求证:BF=AE;
(3)如图3,在(2)的条件下,连接AF,取AF的中点G,连接BG并延长交线段EC于M,交线段AD于R,过点A做AN∥EC交线段BR于N,若GN=2,EM=5,求CM的长.
【答案】(1)见解析;(2)见解析;(3)CM=9.
【解析】
(1)根据三个角是60°的三角形是等边三角形即可证明.
(2)如图2中,作FM∥AC交AB于M.证明△BMF是等边三角形,△EMF≌△CAE(AAS)即可解决问题.
(3)如图3中,连接AM,ER.证明△AGR≌△FGB(AAS),△EBR≌△BEF(SAS),再证明△AMN是等边三角形,证明∠ANR≌△AME(SAS),推出EM=RN=5,证明BR=EF=EC=7即可解决问题.
(1)证明:∵∠D=90°,∠ACD=30°,
∴∠CAD=60°,
∵AC平分∠BAD,
∴∠CAB=∠CAD=60°,
∵AD∥BC,
∴∠DAC=∠BCA=60°,
∴∠B=∠BCA=∠BAC=60°,
∴△ABC是等边三角形.
(2)证明:如图2中,作FM∥AC交AB于M.
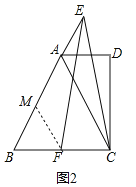
∵MF∥AC,
∴∠BMF=∠BAC=60°,∠BFM=∠BCA=60°,
∴∠B=∠BMF=∠BFM=60°,
∴△BMF是等边三角形,
∴MF=BF,∠EMF=120°=∠CAE,
∵EF=EC,
∴∠EFC=∠ECF,
∴∠MFE=180°﹣60°﹣∠EFC=120°﹣∠EFC,
∠AEC=180°﹣60°﹣∠ECB=120°﹣∠ECF,
∴∠MFE=∠AEC,在△EMF和△CAE中,
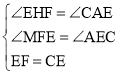 ,
,
∴△EMF≌△CAE(AAS),
∴MF=AE,
∴BF=AE.
(3)解:如图3中,连接AM,ER.
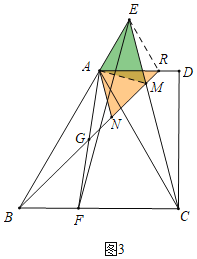
∵AR∥BF,
∴∠ARG=∠GFB,∠EAR=∠ABC=60°,
∵∠AGR=∠FGB,AG=GF,
∴△AGR≌△FGB(AAS),
∴AR=BF,RG=BG,
∵AE=BF,
∴AE=AR,
∴△AER是等边三角形,
∴ER=AE=BF,∠BER=∠EBF=60°,
∵BE=EB,
∴△EBR≌△BEF(SAS),
∴∠BEF=∠EBR,EF=BR,
∵∠BEF=∠ACE,
∴∠ABM=∠ACM,
∴A,B,C,M四点共圆,
∴∠CMB=∠CAB=60°,
∴∠EMR=∠EAR=60°,
∴A,E,R,M四点共圆,
∴∠AMF=∠ARE=60°,
∵AN∥EC,
∴∠ANM=∠NMC=60°,∠NAM=∠AME=60°,
∴△AMN是等边三角形,
∴AN=AM,
∵∠NAM=∠EAR=60°,
∴∠NAR=∠MAE,
∵AR=AE,
∴∠ANR≌△AME(SAS),
∴EM=RN=5,
∵GN=2,
∴GR=GB=2+5=7,
∴BR=EF=EC=14,
∴CM=EC﹣EM=14﹣5=9.


科目:初中数学 来源: 题型:
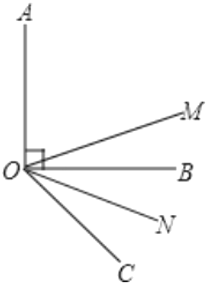
【题目】如图,已知![]() 与
与![]() 互为余角,且
互为余角,且![]() 平分
平分![]() 平分
平分![]() .
.
(1)求![]() 的度数;
的度数;
(2)如果已知![]() ,其他条件不变,则
,其他条件不变,则![]() _______度;如果已知
_______度;如果已知![]() ,其他条件不变,则
,其他条件不变,则![]() _______度;
_______度;
(3)从以上求![]() 的过程中,你得出的结论是__________.
的过程中,你得出的结论是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD=AE,添加下列条件仍无法证明△ABE≌△ACD的是 ( )

A. AB=AC B. ∠ADC=∠AEB C. ∠B=∠C D. BE=CD
查看答案和解析>>
科目:初中数学 来源: 题型:
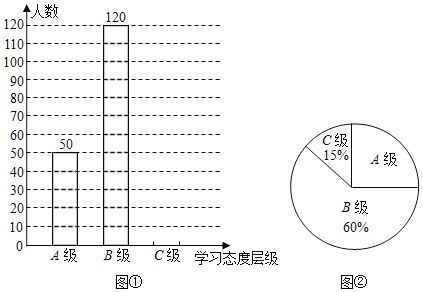
【题目】我校对八年级学生的学习态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了多少名学生;
(2)通过计算达到C级的有多少人?并补全条形图.
(3)根据抽样调查结果,请你估计我市近80000名八年级学生中大约有多少名学生学习态度达标(达标指的是学习兴趣达到A级和B级)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为宣传“扫黑除恶”专项行动,社区准备制作一幅宣传版面,喷绘时为了美观,要在矩形图案四周外围增加一圈等宽的白边,已知图案的长为2米,宽为1米,图案面积占整幅宣传版面面积的90%,若设白边的宽为x米,则根据题意可列出方程( )

A. 90%×(2+x)(1+x)=2×1 B. 90%×(2+2x)(1+2x)=2×1
C. 90%×(2﹣2x)(1﹣2x)=2×1 D. (2+2x)(1+2x)=2×1×90%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC
重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )

A. 3 B. 4
C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题背景)解方程:x4﹣5x2+4=0.
这是一个一元四次方程,根据该方程的特点,我们可以借助“换元法”将高次方程“降次”,进而解得未知数的值.
解:设 x2=y,那么 x4=y2,于是原方程可变为 y2﹣5y+4=0,解得 y1=1,y2=4. 当 y1=1 时,x2=1,x=±1;当 y2=4 时,x2=4,x=±2;
原方程有四个根:x1=1,x2=﹣1,x3=2,x4=﹣2.
(触类旁通)参照例题解方程:(x2+x)2﹣4(x2+x)﹣12=0;
(解决问题)已知实数 x,y 满足(2x+2y+3)(2x+2y﹣3)=27,求 x+y 的值;
(拓展迁移)分解因式:(x2+4x+3)(x2+4x+5)+1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学八⑴班、⑵班各选5名同学参加“爱我中华”演讲比赛,其预赛成绩(满分100分)如图所示:
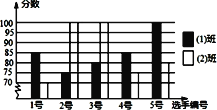
(1)根据上图填写下表:
平均数 | 中位数 | 众数 | |
八(1)班 | 85 | 85 | |
八(2)班 | 85 | 80 |
(2)根据两班成绩的平均数和中位数,分析哪班成绩较好?
(3)如果每班各选2名同学参加决赛,你认为哪个班实力更强些?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com